ezSPC 2.0, R을 이용한 13주차 예제 풀이

문제 1번

 

자동차의 종류에 따라 연비가 서로 다른지 확인하고 싶다.

동급의 자동차 4 종류에 대해 1 리터당 주행거리 (km)를 측정하였다 .
자동차에 따라 연비가 서로 다르다고 할 수 있는가?(유의 수준 5%)

 

 

풀이 

 

인자(Factor)는 자동차, 수준(Level)은 서로 다른 차종을 택하면 된다.

 

 

 

 

칼럼 1은 인자변수, 칼럼 2가 반응 변수

 

 

좌측 하단의 자료를 눌러서 분산분석표를 볼 수 있다.

SSA = 12.9, 자유도는 K-1=3

SSE = 1.72, 자유도는 K(n-1)=14, 반복수가 다르므로 3개 4,4,3 =14

 

p값이 0.05보다 작기 때문에 기각한다.

 

문제 2번

 

회사는 신제품의 가격을 책정하느데 어려움을 겪고 있다. 제품의 가격을 11,000원 11,500원 12,000원 12,500원 13,000원으로 정하고 도시의 크기와 시장 규모가 비슷한 지역의 편의점 50개를 선정하고 10개씩 그룹화 한 다음 1 그룹에서는 11000원에 2,3,4,5 그룹에서는 11,500원 12,000원 12,500원 13,000원에 판매를 시범적으로 5일간 진행하였다 아래의 데이터는 각 편의점별 5일간의 제품의 판매 실적이다. (단위 : 개)

 

각 그룹별 5일간 판매실적 기입

group1=c(10,11,12,9,10,11,13,10,8,10)
group2=c(13,12,13,14,12,15,14,12,13,16)
group3=c(9,8,7,10,9,11,13,10,9,6)
group4=c(10,11,10,10,11,12,9,12,13,10)
group5=c(6,4,5,7,5,4,6,8,4,6)

 

 

Apply 함수를 사용한다. 1인 경우에는 row 별로 계산하는 것이고, column별로 하는 것이기 때문에 2를 사용한다.

 

data=data.frame(group1,group2,group3,group4,group5)
apply(data,2,mean)

 

 

이제 각 그룹 모평균에 대한 95%를 구해서 하나의 그래프에 나타내 보도록 한다.

 

따라서 각 그룹에 대한 t.test를 통해서 평균 값을 가져오도록 한다.

mean_result=c(t.test(group1)$estimate,t.test(group2)$estimate,t.test(group3)$estimate,t.test(group4)$estimate,t.test(group5)$estimate)

각 그룹별 신뢰구간 하한을 정리한다.

lower=c(t.test(group1)$conf.int[1],t.test(group2)$conf.int[1],t.test(group3)$conf.int[1],t.test(group4)$conf.int[1],t.test(group5)$conf.int[1])

각 그룹의 신뢰구간의 상한을 upper 변수에 넣고

upper=c(t.test(group1)$conf.int[2],t.test(group2)$conf.int[2],t.test(group3)$conf.int[2],t.test(group4)$conf.int[2],t.test(group5)$conf.int[2])

x는 각 그룹에 나타노도록 하고

x=1:5

 

그 다음에 data.frame은 아래와 같이 설정한다.

df=data.frame(x,mean_result,lower,upper)

x는 그룹을 나타내고 평균과 신뢰구간의 하한과 상한으로 구성되어있음을 알 수 있다.

 

너무 길어서 짤림

 

1개 그래프에 여러 개의 그림을 동시에 하기 위해서는 ggplot2를 사용해야하는데 ggplot2를 가져오기 위해서 아래와 같이 입력한다.

install.packages("ggplot2")

선택창은 알아서 잘 ok와 국가 및 지역을 누르시고

 

 

설치가 끝나면 위와 같이 나오게 된다.

 

다운로드된 다음에 다시 아래와 같이 입력하여 다음 단계를 위한 준비를 하면 된다.

 

library(ggplot2)

 

ggplot을 하게 되면

 

ggplot(df, aes(x=x, y=mean_result))+geom_point(size=4)+geom_errorbar(aes(ymax=upper,ymin=lower))

아래와 같은 결과가 나오게 된다.

 

 

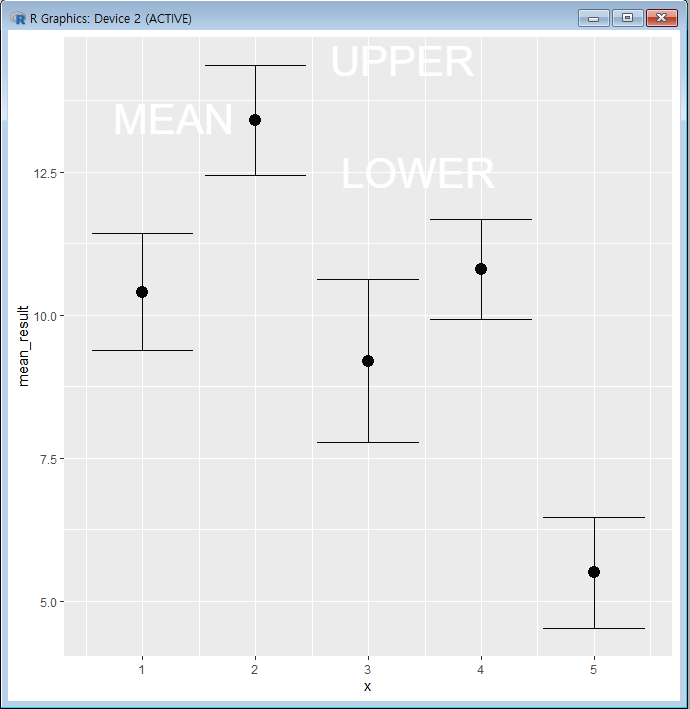
95%의 신뢰구간 상한 및 하한이 I의 꼴로 나옴을 알 수 있고 그 사이에 평균값이 있음을 알 수 있다.

 

이 자료를 토대로 분산 분석을 실시한다.

 

다시 한번 데이터를 그룹핑하고 다음으로 각 데이터들이 그룹별로 반복되어 있다는 것을 보여주기 위해서

 

data=c(group1,group2,group3,group4,group5)
data=data.frame(response=data,group=c(rep(1,10),rep(2,10),rep(3,10),rep(4,10),rep(5,10)))

*(n,10)은 아무래도 각 그룹에 대한 것을 표현하는 것 같다.

 

그 다음에 이 데이터를 이용해서 analysis of variance(ANOVA) 분산분석을 실시한다.

model=aov(response~as.factor(group),data=data)

일원 배치모형을 선택하고 reponse는 각 데이터에서 나온 값들이고 group을 인자 즉 factor 5개 수준으로 구분한 것이다.

 

결과값들을 보여달라 요청하게 되면

summary(model)

 

 

인자는 수준이 5개이기 때문에 자유도가 4 , 총 데이터 개수는 50 총 자유도는 49 인자의 자유도와 오차의 자유도를합하면 전체 자유도가 되기 때문에 전체 자유도 49에서 인자의 자유도 4를 빼주면 오차의 자유도는 45.

 

Sum of Sq 은 각각 331.5 100.5

mean sq 는 각각의 자유도로 나누어 준 것이니 82.88과 2.23 따라서 2.23이 MSE

즉 일원배치법모형에서 오차항 엡실런ij는 평균이 0 분산이 시그마제곱인 정규분포를 따르는데 그 때 시그마제곱에 대한 불편추정량이 바로 2.23

 

검정 통계랑은 MSA/MSE 이므로 F0는 37.11이다.

 

p-VALUE는 아주 작기 때문에 그룹간 모든 평균이 같은가에 대한 귀무가설을 기각하는 것이다. 즉 그룹간의 평균은 차이가 있다 최소한 하나가 다르다는 결론을 받아들일 수 있다.

 

 

문제 3

 

한 생수 제조회사는 5 개 배송업체 (1,2,3,4,5) 와 계약하고 제품을 배달하고 있다 . 마케팅 담당자는 어떤 배송업체가 신속하게 배달하고 있는지 확인하기 위하여 각 배송업체별 거래 실적 중 20 개를 임의로 선택하고 각 거래에 대한 소요시간을 측정하였다 . 데이터는 다음과 같다 .

 

 

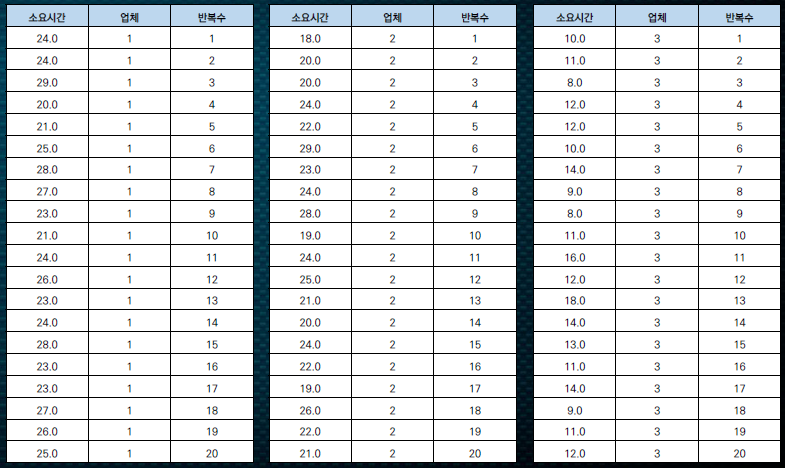
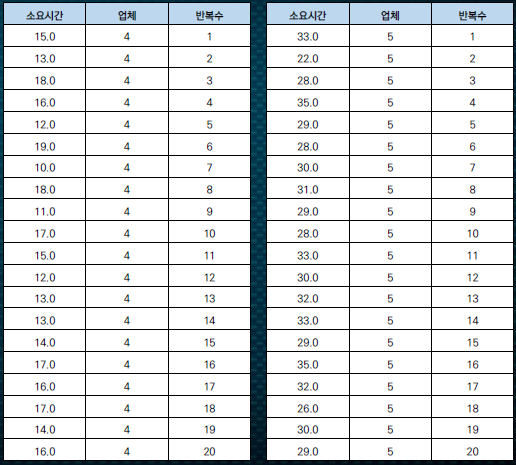
각각의 소요시간을 t라는 범위안에 모두 집어넣어준다.

 

time=c(
24,24,29,20,21,25,28,27,23,21,24,26,23,24,28,23,23,27,26,25,
18,20,20,24,22,29,23,24,28,19,24,25,21,20,24,22,19,26,22,21,
10,11,8,12,12,10,14,9,8,11,16,12,18,14,13,11,14,9,11,12,
15,13,18,16,12,19,10,18,11,17,15,12,13,13,14,17,16,17,14,16,
33,22,28,35,29,28,30,31,29,28,33,30,32,33,29,35,32,26,30,29)

 

그 다음 반복수가 20개이니 20개씩 그룹으로 묶어준다. (각각 그룹을 구분하기 위해)

 

group=c(rep(1,20),rep(2,20),rep(3,20),rep(4,20),rep(5,20))

 

따라서 각 replication은 1그룹에서 20개씩 나누어지는 것이다.

rep=c(rep(1:20,5))

각 5개 열에 대해서 1번부터 20번까지 3개의 변수를 정하고 data.frame을 가져간다.

 

data=data.frame(time,group,rep)

첫번째 컬럼이 time 두번째가 그룹 세번째가 반복수이다.

각 업체별 소요시간을 boxplot 한 페이지에서 서로 비교 하는 것을 보겠다.

boxplot(data[data$group==1,'time'],
data[data$group==2,'time'],
data[data$group==3,'time'],
data[data$group==4,'time'],
data[data$group==5,'time'])

 

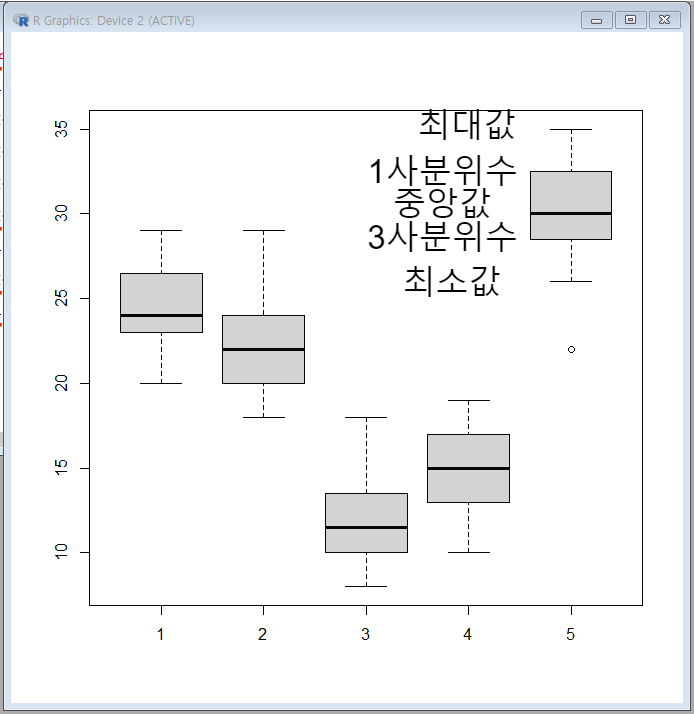
다음으로 배송업체 간 평균 거래 소요시간이 동일한지 유의 수준 5%에서 검정하도록 한다.

summary(aov(time~as.factor(group),data=data))

time 그리고 인자를 group으로 해서 이 데이터에 대한 aov 분산분석을 실시하고 결과를 본다

 

 

 

인자의 수준 수가 배송업체 5개니까 5-1=4의 자유도를 가지고

 

20개 데이터를 수집했으니 100개, 따라서 총 자유도는 99-인자 자유도 4 하니 95가 나온다

그 이후 결과에 대해서는 위에 이전 예제에 설명이 되어 있으니 생략하도록 한다.

 

 P-VALUE는 0에 가까운 값이 나옴으로 기각된다.

하단에 ***는 유의수준이 0.001이라 할지라도 기각되는 것이다. 사후 작업으로 다중비교를 해야한다 

다중비교에 대해서는 14주차 정리에 올라올 예정이다.