식이 설명하는 의미를 중점적으로 넘어가면 어렵지 않다고.... 한다
소개 (Introduction)
플라즈마 매질(medium)은 복잡하다.
- 외부 전기장(E), 자기장(B) <-> Charge particles
- the resulting self-consistent system은 비선형이고 해석하기 어렵지만 어떤 상황에서 선형화 할 수 있다
(특히 플라즈마에서의 파동(wave)들을 다룰 때)
- 상호 충돌
쉽게 보기 위해선 거시적으로 본다. (평균된 속도 분포를 생각함)
맥스웰 방정식 복습(Review of Maxwell`s Equation)

전기장의 다이버전스(∇◦) 는 전하 밀도, 관심있는 표면의 전하는 발산하는 전기장을 만들어낸다.
여기서 다이버전스(∇◦) 발산 연산자이고, E는 전기장, ρ는 표면 전하이다.

유도기전력과 유도전류는 자기장의 변화를 상쇄하려는 방향으로 발생한다.
(회전하는 전기장과 시변하는 자기장은 반대 방향으로 유도된다.)

발산하는 자계 강도(H)는 없다

회전하는 자계 강도(H)는은 시변하는 전기장(변위 전류)와 전류밀도(J)의 합이다.

전류 보존식은 아래와 같다.

식 6을 통해 시간에 따라 변하는 표면 전하와 발산하는 전류 밀도의 합은 0이며 여기서 전류밀도는 전도(conduction) 전류 밀도는 자유 전하의 motion으로 인한 것, 분극(polarization) 전류 밀도는 유전 물질 내 경계 전하의 운동(motion)에 의한것, 자화(magnetization) 전류밀도는 자성 물질 내 자기 모멘트(magnetic moments)에 의한 것이다.
진공(vacuum)에서의 플라즈마에선 두 전류 밀도(J_pol, Jmag )는 0이다.
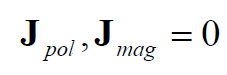

From eq. (8), Charge is conserved.
총 전류(전도 + 변위)는 x의 무관하다.

플라즈마를 발생기키기 위한 전원 (Vrf)이며 CCP를 등가 회로로 만든 것이다. (그림 1)

그림 1을 통해 쉬스(Sheath)에는 변위 전류, 불균일한 플라즈마에는 전도(conduction) 전류가 흐른다.
그림 1의 총 전류밀도는 식9임을 알 수 있다.
폐루프에 KVL을 적용하면 식 10이 나온다.

로렌츠의 힘
플라즈마 내의 전자와 이온은 전기장과 자기장이 있을 때 로렌츠의 힘을 받게 된다.

전기장과 자기장에 나타난 힘을 나타낸 것이다.
(생각해 보자) 전자가 ICP 구조에서 안테나가 있고, 매칭회로를 통해 전류가 흐를텐데 유도 B 필드가 생기고 유도 E 필드가 생긴다. 그럼 전자가 움직이면서 전류가 생기고, 유도 E, B 필드를 만들들고 힘을 다시 만들고 또 다시 전자기 움직이면서 무한히 반복된다 이를 그림 2와 같이 표현이 가능하다.

보존 방정식 (Conservation Equation)
어떤 공간이 주어지는데 특정 시간 t에 위치 r, 속도 v가 변하는 것,
x라는 위치 속도 vx 한 축에서 표현을 한 것, 미소 공간 dx/dvx에서 구하는 것..? f라는 함수는 시간에 따라 변하고, 위치, 속도에 따라 변하는 것
c는 collision에 관한것, F/m은 가속도를 벡터로 나타낸 것이다
particle density
particle flux
particle 위치 에너지??
'그 외 전공 > 그 외 전공 통합 글' 카테고리의 다른 글
| 전기력(Electric Force)와 전계(Electric Field)에 대해 (0) | 2022.03.19 |
|---|---|
| 전하(electric charge)란 무엇일까? (0) | 2022.03.14 |


댓글