밀러 효과
하나의 부유(Floating) 임피던스를 2개의 접지된 임피던스들로 변환 시키는 방법이며, 부유 임피던스가 커패시터인 경우 각 노드에 하나의 극점을 연관시키도록 변환하는 방법이다.
이 부유 임피던스는 입력 임피던스를 낮춰주고 출력 임피던스를 높여주게 된다.
밀러 이론 해석

사진 1에서의 회로는 부유 임피던스를 사진 2와 같이 2개의 접지된 임피던스로 변환시키는 방법을 알 수 있게 하고, 해당하는 임피던스가 극점을 가지고 있는 임피던스(대부분 기생 Cap)가 각 노드에 하나의 극점을 연관시키도록 하는 것이다.
여기서 사진 2는 밀러이론을 이해하기 쉽게 그려진 일반적인 회로라고 생각하면 된다. 구성은 사진 1과 비슷한 구조임을 이해해야 한다.
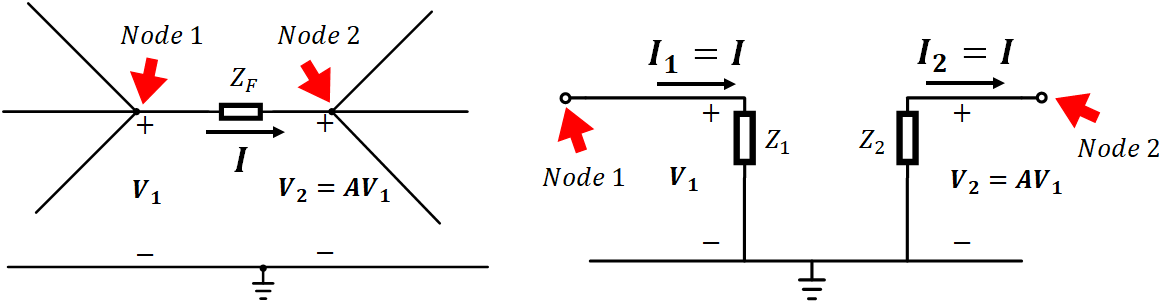
사진 2. 에서 노드 1의 전압인 V1 과 노드 2의 전압인 V2에 대해 V2=AV1으로 관계 되는 것이 어떻게든 정해졌다고 가정을 하지만 밀러 정리를 위한 가정은 아니니 참고바라며 이득 인수인 A는 음이거나 양의 값일 수 있고 1보다 큰 크기를 갖는다. 이 내용은 증폭기와 비슷한 식을 가짐을 생각하라 [모르겠다면 하단의 링크]
2021.07.02 - [회로 해석 기초 지식/Basic] - 전자회로에서 표현하는 증폭기란?
전자회로에서 표현하는 증폭기란?
이번 포스팅에서는 증폭기란 개념에 대해 알아보도록 하겠습니다. 목차는 아래와 같습니다. 목차 1. 증폭기는 왜 필요할까? 2. 증폭기의 심볼과 수식 3. 데시벨(decibel) 표현 증폭기는 왜 필요할까?
doctorinformationgs.tistory.com
해석을 하는데에 있어 가장 중요한 고찰이 있다.
1) 노드 1로부터 피드백 임피던스(ZF)로 존재를 알 수 있게 하는 방법은 노드 1로부터 Z로 흐르는 전류는 I는 Z1과 동일해야한다.
2) 노드 2에 주입된 전류(I)는 Z2에 의해 주입되는 전류와 동일해야한다.
고찰 1과 사진 2를 통해 노드 1에 흐르는 전류는 아래 식 (1)로 표현된다.

식 (1)의 전압 강하가 V1-V2인 이유는 노드 1에서의 전류를 계산하기 때문에 (V1-V2)/ZF가 됨을 유의하자.
고찰 2와 사진 2를 통해 노드 2에 흐르는 전류는 아래 식 (2)로 표현한다.

식 (2)의 Z2가 음의 부호를 가지는 이유는 위에서 언급한 고찰에서 노드 2에 주입된 전류 즉 노드 1로부터 나오는 전류이기 때문에 식(1)과 동일하게 (V1-V2)/ZF 가 되며 이는 노드 2에서 흐르는 전류의 반대의 극성을 가지기 때문에 음의 부호를 가지고 나오게 된다.
Z1을 구하기 위해서 식(1)을 이용해 Z1에 대한 식으로 계산하는 과정은 아래와 같다.


V1을 입력이라 생각하고, V2를 출력이라 생각해보자 따라서 식 (3) V1에 대해 나누어보면 전압 이득식으로 표현이 된다.(대게 피드백 임피던스는 한쪽의 노드는 입력, 다른 한쪽의 노드는 출력에 있음을 알 수 있기 때문에 전압 이득식으로 표현이 가능하다.)
또한 사진 1을 통해 Z1에 대해 생각해 보면, Z1을 입력 임피던스로 볼 수 있다. 따라서 밀러 이론을 통해 입력 임피던스는 전압이득에 의해 낮아짐을 알 수 있다.
Z2도 위 방법과 동일하게 계산하면 아래와 같다.


위 과정과 동일하게 식 (5)를 V2로 나누어보면 전압이득의 역수가 되며 위와 동일한 과정을 하게 되면 Z2는 전압이득의 역수 이기 때문에 출력 임피던스가 커짐을 알 수 있다
Z1과 Z2가 커패시터라고 하면 Z1 Z2는 아래와 같이 표현이 가능함을 알려줄 수 있으며 피드백 커패시터(또는 부유 커패시터)로 인해서 Z1은 (1-Av) 배, Z2는 (1-1/Av) 배가 됨을 알 수 있다.
여기서 전압이득 Av 는 직류 이득을 의미하게 된다.
전자회로 2 과정을 학습하셨습니다.
아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.

2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼
전자회로 2 커리큘럼
전자회로 2 커리큘럼입니다. 전자회로 2에 대한 간략한 설명은 아래와 같습니다. 전자회로 1에서 배웠던 능동소자(Diode, BJT, MOSFET)에 대해 학습했으며 그에 대한 다이오드 회로 및 단일 증폭기인
doctorinformationgs.tistory.com
'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 소신호 등가모델(Small Signal Equivalent Model)에 알아보자 (0) | 2021.10.09 |
|---|---|
| 다이오드 회로의 일정전압모델 해석 (4) | 2021.10.02 |
| 이상적인 다이오드 회로의 이해(회로기초, 측정을 통해 이해해보자) (0) | 2021.10.02 |
| MOSFET의 동작영역을 알아보자 (0) | 2021.09.28 |
| 아날로그 회로설계 개요 (0) | 2021.09.01 |



댓글