지난 포스팅에서 다중비교에 대한 언급을 간략하게 했었다.
이에 대해서 조금 더 심도 있게 알아보고자 한다.
2021.12.01 - [고등 수학/확률과 통계] - 13주차 정리 - 일원배치법, 분산분석, 다중비교
13주차 정리 - 일원배치법, 분산분석, 다중비교
일원 배치법 인자가 하나이고 수준수가 a개인 일원 배치법을 한번 보도록 한다. 일원 배치법 통계적 모형 일원 배치법도 통계적 모형으로 나타내면 아래와 같다. µ_i는 i번째 수준의 평균, y_ij는
doctorinformationgs.tistory.com
다중비교
다중비교(Multiple Comparison)의 방법
1) 최소유의차(least significant Difference)
가장 검정력이 뛰어난 피셔의 최소유의차
‣ pairwise(모든 수준들 간에 두 수준별 평균비교 검정을 하는 방법)
‣ 3 개 그룹의 평균들을 비교할 때 적절한 방법 (세개 이상의 그룹들에 대해서 pairwise 비교하여 검정하는 것이 효과적이다)
모평균차에 대한 신뢰 구간을 구할 때 오차 한계가 변하지 않기 때문에 최소유의차라 함
2) Tukey’s HSD(honestly significant difference)
‣ 모든 집단들의 표본수가 같을 때 사용하는 방법으로 한 개의 기준치(컨트롤 그룹)를 사용하여 1 대 1 의 짝의 비교를 하는 방법
‣ 컨트롤 그룹과 각 다른 그룹들 간에 비교할 때 사용
3) Newman-Keuls
‣ 평균치들을 낮은 것에서 큰 순서대로 등위를 지어서 비교하는 방법, 제일 작은 것과 그 다음 그 다음에 또 제일 작은 것과 그 다음 이런식으로
예를 들어 첫번째 두번째 첫번째 세번째 첫번째 네번째 첫번째 다섯 번째 ... 이렇게 등위간 비교하는 방법을 쓸 때 이 방법을 사용한다.
4)SNK(Student-Newman-Keuls)
‣ 표본의 평균을 크기 순서에 따라 다수의 범위를 이용하여 신뢰구간을 구하여 모집단 평균간의 차이에 대한 검정만을 할 수 있는 절차
5) Duncan
‣ 귀무가설을 기각할 확률이 매우 높으며 , 전체적인 동질성 집단의 유무를 가리는 것에 목적 동시검정 을 둔 경우에 사용하는 방법
‣ p-value 가 아주 작은 경우 에 전체적인 동질성 집단의 유무를 가리는 것에 대한 동시 검정을 할 때에 주로 사용
6) Bonferroni’s Adjustment
‣ 그룹의 수가 k 개이라면 비교할 pair 의 수 (k(k-1)/2) 가 그룹간의 degrees of freedom(d.f) (k-1) 보다 큰 경우에 사용하는 검정법
‣ 사전에 관심있는 두 집단에 대한 검정에 유용
예를 들어서 만약에 우리가 5개 수준이 있으면 10개의 두 그룹 비교를 해야하는데 다 하는게 아니라 몇 개 관심있는 집단에 대해서만 차이 비교를 하고 싶을 때 사용

7) Seheffe’s 검정법
‣ 집단들의 표본수가 아니어도(같지 않더라도) 사용할 수 있는 방법
‣ 대비까지 고려하여 모든 가능한 집합에 대하여 동시에 적용(다중 비교) 할 수 있는 신뢰구간을 제공
8) Dunnett’s test
‣처리효과의 수준 하나가 control(실험집단) 인 경우의 집단과 다른 집단들을 pairwise 비교할 경우 사용
어느 한 방법이 모든 면에서 완벽할 수 없기 때문에 목적에 따라 조금씩 변화가 되기 때문에 내용들을 충분히 수용해서 다양한 방법들이 소개된다.
그러나 뛰어난 방식에 대해 나열 하자면 아래와 같다

𝜇1,𝜇2,𝜇3,𝜇4에 대한 다중비교
𝜇1,𝜇2,𝜇3,𝜇4에 대해서 동일성을 보는데 기각이 되기 때문에 다중 비교를 하게 된다.

t_dfE(오차항 자유도), SP제곱 대신에 mse를 쓴다.


이 신뢰구간이 0 을 포함하면 두 모평균은 같다고 할 수 있음
만약에

n_i, n_j가 n이 됨을 알 수 있다. 이 때 x_i^(bar) - x_j^(bar)는 각각의 수준에 따라서 표본평균값이 달라지지만 뒤에 나오는 오차한계 부분은 공통이다. 이 공통 부분을 LSD라 한다.

그래서 각각의 표본평균차가 절댓값을 구한 다음에
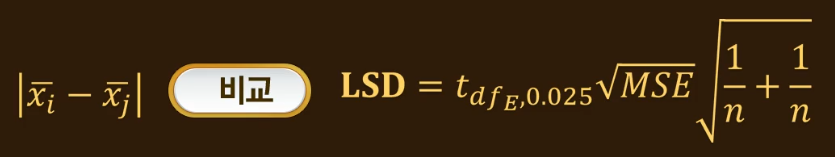
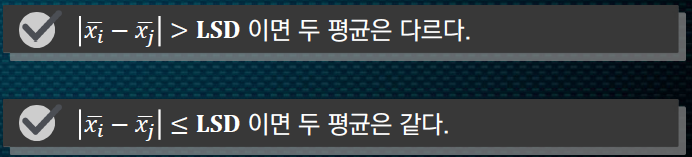
같을 때는 두 신뢰구간이 0을 포함하기 때문이다.
예제 문제는 아래의 링크를 통해 풀 수 있다.(문제 1번)
2021.12.02 - [분류 전체보기] - R을 이용한 14주차 예제 문제풀이
R을 이용한 14주차 예제 문제풀이
문제 1번(13 주차 문제3과 동일한 문제이다. 따라서 다중 비교 문제에 대해서만 설명하겠다) 2021.12.01 - [시뮬레이션 툴(Simulation Tool)/R, ezSPC] - ezSPC 2.0, R을 이용한 13주차 예제 풀이 ezSPC 2.0, R을..
doctorinformationgs.tistory.com
'고등 수학 > 확률과 통계 개인학습 노트' 카테고리의 다른 글
| 적합도검정(카이제곱 검정), 비모수검정, 다변량분석 소개 - 15주차 정리 (0) | 2021.12.10 |
|---|---|
| 14주차 정리 - 대비, 요인 배치법 (0) | 2021.12.03 |
| 13주차 정리 - 일원배치법, 분산분석, 다중비교 (0) | 2021.12.01 |
| 13주차 정리 - 실험계획법 소개, 원리, 순서 (0) | 2021.11.30 |
| 구간 추정 - 9주차 정리 (0) | 2021.10.29 |




댓글