대비(Contrast)
4개의 수준이 있을 때 네번 째 수준의 평균과 123 수준의 평균의 평균과 같은지 비교해보고자 할 때 아래와 같이 가설을 세울 수 있다.

L은 각각의 곱과 각 모평균을 더할때 앞에 있는 계수들의 합이 0이면 이러한 모평균들의 수준 평균들의 선형함수를 대비라고 한다.

이를 풀어 보면

대비 L의 변동
µ_i 대신에 그것의 추정량인 x_i^(bar)를 대입하고 그 다음에 세타는 Sum of Ci^2 하면 각 대비의 변동은 자유도가 1인 카이제곱분포를 따른다.

따라서 귀무가설을 L이 이냐 H0:L=0 이냐 H1:L은 0이 아니냐고 할 때 검정 통계량 F0는 SL/MSE
이는 자유도가 1 두번째 자유도는 오차항 자유도 dfE를 갖는 F 분포를 따른다.

직교 대비

각각의 대응되는 계수들 Ci*di를 다 합해서 이것이 0이 되면 L1과 L2는 직교 대비라고 한다.(서로 공통된 부분이 없다는 의미)

요인 배치법
‣ 대비의 개념을 활용
‣ 요인배치법을 사용하는 경우

‣ 요인배치법을 통해 최소의 실험을 가지고 최대의 효과를 얻을 수 있음
‣ 인자들의 수가 많을 때 다원 배치법 사용
‣ 단 반복하는 경우에는 실험 횟수가 굉장히 많아짐
--> 이럴 때 요인배치법을 사용

모든 인자 수를 2개로 제한하는 경우를 "2수준계 요인배치법"이라 하고,
인자 수준을 3개로 제한하는 경우는 3수준계 요인비치법이라고 이야기한다.
2^2 요인 실험
가장 최소의 요인 실험

밑 숫자 2는 인자의 수준 수이며, 2제곱은 인자의 수를 이야기한다.

실제로 실험에 적용하는 실험 조건은 하나하나씩 따로따로하는게 아니라 A0B0를 한 실험조건 A1B0 ... A1B1을 각각 실험 조건으로 한다. 규칙으로 아래와 같이 표기한다.

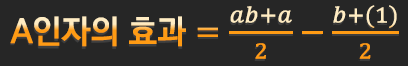
높은 수준에서의 평균값 - 낮은 수준에서의 평균값
B인자는 전혀 상관하지 않았으므로 이를 A 주효과 (A main effect) 라 함
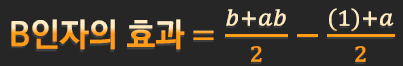
B의 높은 수준에서의 평균값 - B 의 낮은 수준에서의 평균값
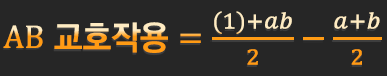
A와 B 가 같은 수준일 때의 평균 - A 와 B 가 서로 다른 수준일 때의 평균
실험 조건의 평균과 대비를 아래와 같이 표현 가능하다.

위에서 언급했던걸 학습해보면 A의 주효과는 아래와 같다.

앞에 1/2만 고려하여 모두 더했을 때 0이 나옴으로 대비이다.
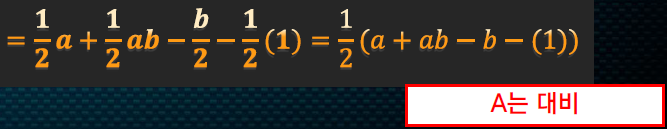
B인자 효과와 AB 교호작용도 각각 확인해 보면 전부 다 대비임을 알 수 있다.
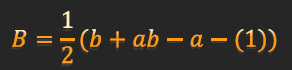

A,B 직교 대비는

이므로
(1)의 계산 과정은 (-1/2)(-1/2)
(a)의 계산 과정은 (1/2)(-1/2)
(b)의 계산 과정은 (-1/2)(1/2)
(ab)의 계산과정은 (1/2)(1/2)
따라서 이 총 합이 0이 됨으로 A와 B는 직교 대비이다. 위 B인자의 효과 AB 교호작용을 적용시켜 풀 수 있다.
정리하면 아래와 같다.


위에서 언급한 변동의 내용과 A의 주효과의 제곱을 한 것이 S_LA가 되는 관계를 가지고 있다.
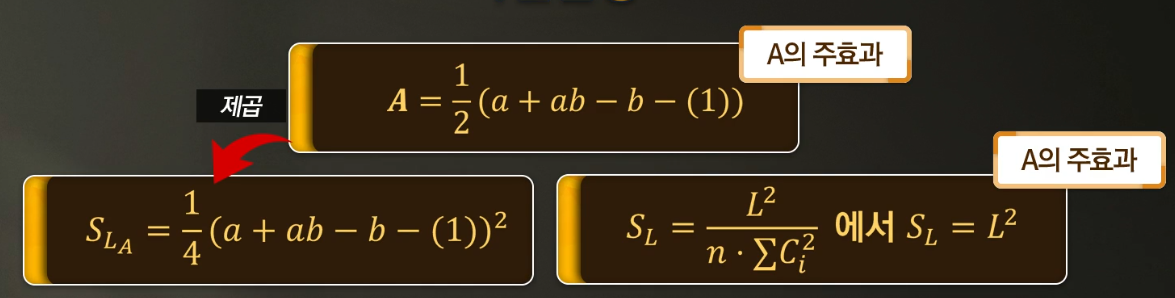
검정 통계량의 분포는
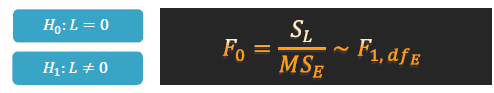
2^3 요인 배치법
인자 A,B,C (3개)
수준 수 2개를 의미하는 것이다.
해당 포스팅의 예제 문제는 문제 2번부터 시작됩니다.
예제 문제로 넘어가실려면 하단의 링크를 타고 들어가시면 됩니다.
2021.12.02 - [분류 전체보기] - R을 이용한 14주차 예제 문제풀이
R을 이용한 14주차 예제 문제풀이
문제 1번(13 주차 문제3과 동일한 문제이다. 따라서 다중 비교 문제에 대해서만 설명하겠다) 2021.12.01 - [시뮬레이션 툴(Simulation Tool)/R, ezSPC] - ezSPC 2.0, R을 이용한 13주차 예제 풀이 ezSPC 2.0, R을..
doctorinformationgs.tistory.com
'고등 수학 > 확률과 통계 개인학습 노트' 카테고리의 다른 글
| 적합도검정(카이제곱 검정), 비모수검정, 다변량분석 소개 - 15주차 정리 (0) | 2021.12.10 |
|---|---|
| 14주차 정리 - 다중 비교 (0) | 2021.12.02 |
| 13주차 정리 - 일원배치법, 분산분석, 다중비교 (0) | 2021.12.01 |
| 13주차 정리 - 실험계획법 소개, 원리, 순서 (0) | 2021.11.30 |
| 구간 추정 - 9주차 정리 (0) | 2021.10.29 |




댓글