일원 배치법
인자가 하나이고 수준수가 a개인 일원 배치법을 한번 보도록 한다.
일원 배치법 통계적 모형
일원 배치법도 통계적 모형으로 나타내면 아래와 같다.

µ_i는 i번째 수준의 평균, y_ij는 i번째 수준 j번째 반복의 반응 값이 된다.
앱실론 ij는 y_ij에 관여하는 오차항이 되겠고 물론 이 오차항도 iid 노멀 평균 0 분산 시그마 제곱으로 한다,
y_ij에 대해 다시 써보면


이것을 전체 평균 뮤를 보면 뮤를 더하고 빼는 것이니까 식의 차이가 없고 µ_i-µ를 수준효과라고 이야기 한다.
µ_i-µ 는 각각의 수준이 전체평균과 어떠한 차이가 나는지 수준별 효과가 된다.



분산 분석
분산 분석을 하기에 앞서서 전체 총 변동은 따지고 보면 요인 A,B 또는 AB 교호작용에 의한 변동 오차에 의한 변동으로 나눠지기도 한다. 따라서 분산 분석을 할 때 어떤 Y의 총 변동이 어떠한 변동의 요소로 분리되느냐 이 분리 작업이 중요하다. 이것을 이용해 우리는 평균의 차를 점검하기도 하고 수준간의 차이가 있다 없다 등등을 이야기하게 된다.


분산 분석의 가정

이 이야기는 앱실론_ij는 iid 놈ㄹ 평균 0 분산 시그마 제곱인 이야기를 하고 있는 것이다.
분산 분석의 변수와 요인

종속 변수는 반응값을 이야기함, 인자는 독립변수
분산 분석의 절차
가설수립은 아래 H0와 같다.
대립 가설은 H1은 최소한 한 평균은 같지 않다.

분산분석 F 검정을 하게 되고, 만약의 모든 평균들이 같아서 즉 F 검정에서 P value가 0.05보다 큰 값이 나와서 기무가설을 기각하지 못하면 결론은 간단하다 모든 수준별평균 같고 종료한다.

만약에 분산분석에서 F 검정에서 P value가 알파 값보다 작게 나와서 기무가설을 기각하게 되는 경우 대립 가설에서는 구체적인 답을 주지 않는다.

일원분산분석(One-Way ANOVA ... Analysis Of VAriace)
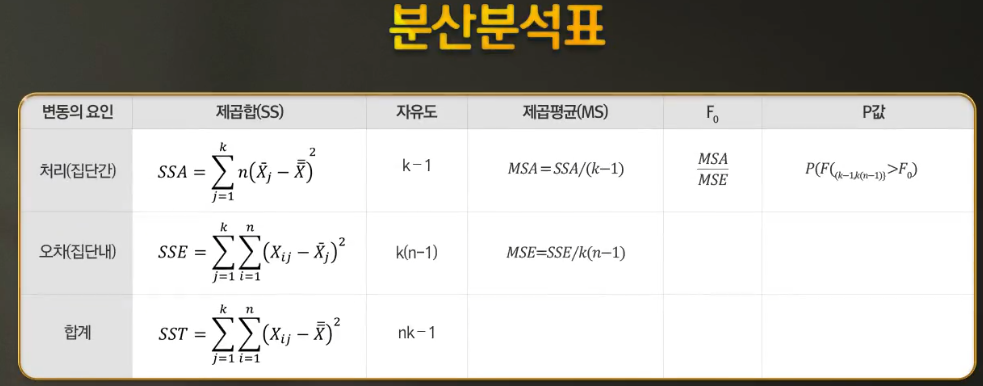
총 변동 SST는 데이터를 X_ij로 표현한다면 위 사진에서 확인 할 수 있다.
수준 1,2,3 의 차이를 SSA로 보고, 같은 수준인데도 X_ij 값들이 다르게 나온 경우 SSE라 한다 SST=SSA+SSE
SSA의 자유도는 수준수가 몇 개냐 수준수 빼기 1이 된다 (K개의 수준수가 있는 경우 K-1)
SST는 전체데이터 빼기 1, 각 수준별로 n개씩 반복했기 때문에
SSE는 인자 수준수 K 곱 각 수준별로 n-1개
제곱평균(Mean-Square, MS)
귀무 가설을 판정하기 위한 검정통정계량은 F 분포를 따르고 F0값은 MSA/MSE이다
다중비교(Multi Comparison)
분산분석에서 모든 모평균의 동일성을 나타내는 귀무가설이 기각된 경우 어떤 평균이 차이가 있는지를 확인하는 통계적 방법


다중비교의 방법
1) 최소유의차(least significant Difference)
‣ pairwise( 두 수준별 평균비교 검정을 하는 방법)
‣ 3 개 그룹의 평균들을 비교할 때 적절한 방법
2) Tukey’s HSD(honestly significant difference)
‣ 모든 집단들의 표본수가 같을 때 사용하는 방법
‣ 한 개의 기준치를 사용하여 1 대 1 의 짝의 비교를 하는 방법
3) Newman-Keuls
‣ 평균치들을 낮은 것에서 큰 순서대로 등위를 지어서 비교하는 방법
4)SNK(Student-Newman-Keuls)
‣ 표본의 평균을 크기 순서에 따라 다수의 범위를 이용하여 신뢰구간을 구하여 모집단 평균간의 차이에 대한 검정만을 할 수 있는 절차
5) Duncan
‣ 귀무가설을 기각할 확률이 매우 높으며 , 전체적인 동질성 집단의 유무를 가리는 것에 목적 동시검정 을 둔 경우에 사용하는 방법
6) Bonferroni’s Adjustment
‣ 그룹의 수가 k 개이라면 비교할 pair 의 수 (k(k 1)/2) 가 그룹간의 degrees of freedom( d.f ) (k 1) 보다 큰 경우에 사용하는 검정법
‣ 사전에 관심있는 두 집단에 대한 검정에 유용
7) Seheffe’s 검정법
‣ 집단들의 표본수가 아니어도 사용할 수 있는 방법
‣ 대비 ( 까지 고려하여 모든 가능한 집합에 대하여 동시에 적용 다중 비교 할 수 있는 신뢰구간을 제공
8) Dunnett’s test
‣처리효과의 수준 하나가 control( 실험집단 인 경우의 집단과 다른 집단들을 pairwise 비교할 경우 사용
다중비교 방법의 검정력

해당 주차의 문제는 아래의 링크에서 확인할 수 있다.
2021.12.01 - [시뮬레이션 툴(Simulation Tool)/R, ezSPC] - ezSPC 2.0, R을 이용한 13주차 예제 풀이
ezSPC 2.0, R을 이용한 13주차 예제 풀이
문제 1번 자동차의 종류에 따라 연비가 서로 다른지 확인하고 싶다. 동급의 자동차 4 종류에 대해 1 리터당 주행거리 (km)를 측정하였다 . 자동차에 따라 연비가 서로 다르다고 할 수 있는가?(유의
doctorinformationgs.tistory.com
감사의 글
소정의 지식을 쌓는데에 도움이 되셨다면 광고 클릭을 하여 불쌍한 대학원 노예에게 10원의 기부를 부탁드립니다.
'고등 수학 > 확률과 통계 개인학습 노트' 카테고리의 다른 글
| 14주차 정리 - 대비, 요인 배치법 (0) | 2021.12.03 |
|---|---|
| 14주차 정리 - 다중 비교 (0) | 2021.12.02 |
| 13주차 정리 - 실험계획법 소개, 원리, 순서 (0) | 2021.11.30 |
| 구간 추정 - 9주차 정리 (0) | 2021.10.29 |
| 모멘트 방법, 베이지안 추정, 점추정량의 판정기준 - 7주차 정리 (0) | 2021.10.20 |




댓글