해당 내용은 OP-amp 미분기 적분기, 회로의 주파수 응답, 피드백 단원 이후에 주파수 보상 및 안정성 내용을 읽기 전에 읽어야 하는 내용입니다.
크기(Magnitude)에 대해 읽으시려면 처음부터 읽으시고
위상(Phase)에 대해 읽으시려면 아래 "Chapter 12 주파수 보상 및 안정성" 부분을 읽으시기 바랍니다
원래는 자세히 적으려 했으나 회로를 해석하는데에 있어 중요한 부분만 설명하려 한다.
해당 내용만 완벽하게 알아도 회로를 이해하는데에 있어서 아무런 지장이 없다.
전달 함수와 주파수 응답과의 관계
회로의 전달함수는 다음과 같이 쓸 수 있다.

A0는 낮은 주파수 이득을 이야기하며 흔히 DC 이득(직류 이득) 이라고도 불린다.
이해를 돕기 위한 예로 공통 소스(CS)인 경우 우리가 배웠던 gmRd가 해당이 된다.
분모에 위치해 있는 것은 극점(Pole), 분자에 위치한 것은 영점(Zero)이다. 이는 뒤에서 언급 될 보데의 법칙에서 자세히 다룬다.
회로의 입력이 정현파의 형태라면 출력은 다음과 같이 얻어진다.

H(jω)는 s=jω를 대입하여 얻을 수 있다. 크기와 위상은 회로의 주파수 응답을 나타낸다.(ω=2πft)
회로의 주파수 응답 단원에서는 "크기"에 관심이 있고, 피드백 또는 발진기 단원에서는 "위상"에 관심이 있다.
위상은 아래에 적어놓았으니 "크기"에 대한 예시를 보도록 하자
어떤 회로의 이득은 아래와 같다.
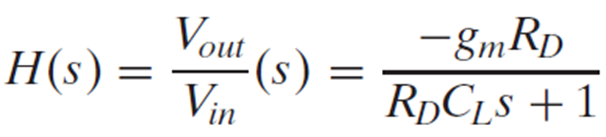
식 3을 "크기"로 표현하면 아래와 같이 된다.

식 4에서 s=jω 이고 j^2은 -1 이지만 절댓값을 넣었기 때문에 1이 됨을 알 수 있다.
복소수 a+jb의 절댓값은 a^2+b^2의 루트를 씌운 것을 기억하자 (페이저)
낮은 주파수의 이득은 커패시터(CL)은 임피던스가 높기 때문에 무시되어 gmRd가 된다. 하지만 주파수가 증가하면서 jb의 항이 1에 가까워짐에 따라 감소함을 알 수 있다.
ω=1/(RC)이 되면 이득은

식 5와 같이 되고 20log를 취하게 되면 -3 dB 감소함을 알 수 있다. 따라서 대역폭을 알고 싶을 때 -3dB 주파수는 이득이 -3dB 떨어지는 지점까지의 대역폭을 말하는 것이다.

보데의 법칙
보데의 법칙은 아래와 같이 간략하게 설명 가능하다.
- 전달함수의 크기의 기울기는 각주파수(ω)가
3-1) 극점 주파수를 지나면서 20 dB/decade로 감소
3-2) 영점 주파수를 지나면 20 dB/decade로 증가.
극점과 영점
단일 극점 시스템의 결과인 식 3을 통해 식 1의 꼴로 만들어 보고 주파수 변화에 따른 그래프를 통해 알아보자
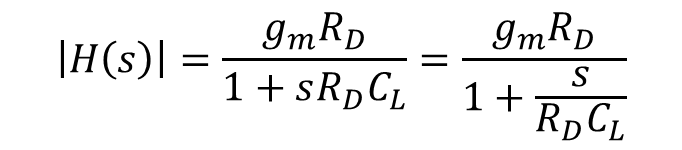
식 6의 분자는 영점이 없고 dc 이득만 있으며 분모에는 하나의 극점(ωp)이 있음을 알 수 있다.
따라서 극점은 아래와 같다.
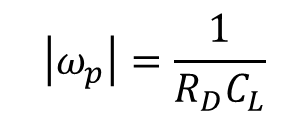
식 6에서 s=jω를 대입하고 주파수가 증가하다가 ωp을 지나면 20 dB/decade로 감소함을 알 수 있다. 이를 도시해보면
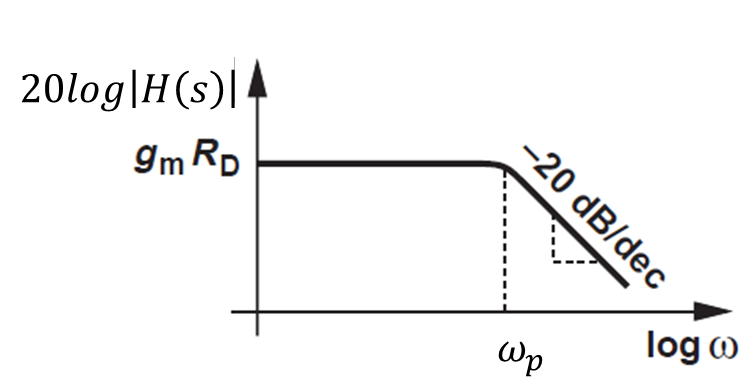
그림 2와 그림 1의 차이는 기울기가 0이고, 극점 주파수에서 -3 dB 주파수 감소를 무시하지만 간략하기 때문에 편한 장점을 제공한다.
Chapter 12
주파수 보상 및 안정성에 대한 관련 내용
기존 회로의 주파수 응답을 알아보았을 때는 "크기"를 중요하게 여겼음을 알 수 있다. 하지만 피드백 챕터의 뒷 부분은 위상에 대해 다루기 때문에 이 내용들을 알아야 한다.
위 내용들을 다시 정리하면
전달함수 H(s)의 크기(magnitude)
극점(Pole)을 지나면 20 dB/dec 로 감소
영점(Zero)을 지나면 20 dB/dec 로 증가
전달 함수의 위상(Phase)
라플라스 변환을 상기하고 극점과 영점은 좌반면(Left Half Plane)에 있다고 가정하고 전달 함수의 위상은
극점(Pole)
극점 주파수의 1/10 부터 감소하기 시작해서 극점 주파수에서 -45° 로 바뀌고 극점 주파수의 10배에서 거의 -90° 로 바뀐다.
영점(Zero)
영점 주파수의 1/10 부터 증가하기 시작해서 영점 주파수에서 +45° 로 바뀌고 영점 주파수의 10배에서 거의 +90° 로 바뀐다.
위 극점과 영점의 위상에 대한 설명은 아래 간단한 예시(그림1)를 통해 알 수 있다.
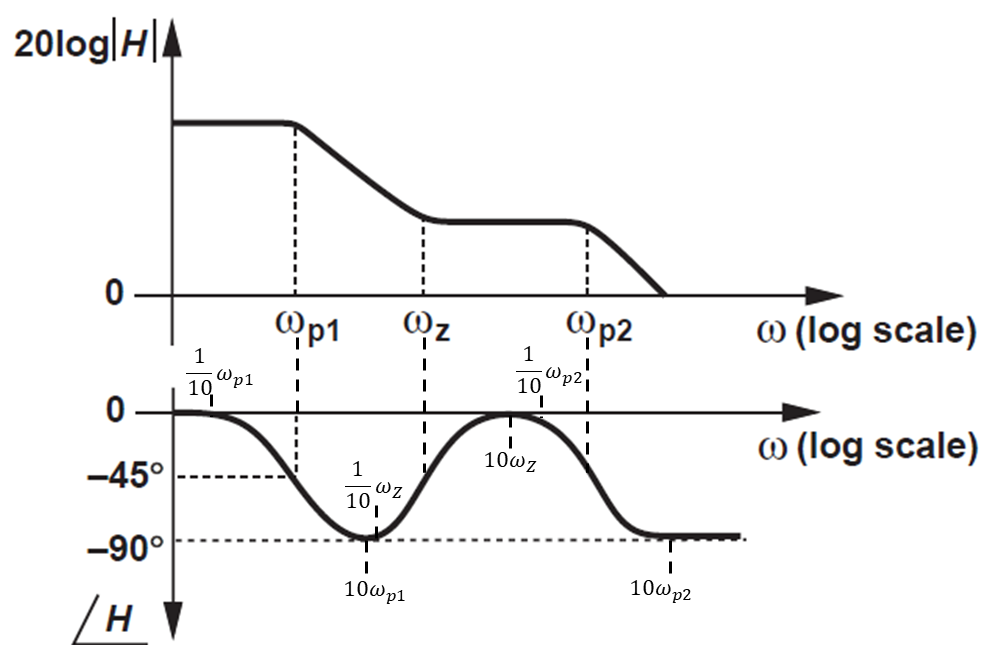
발진에 관한 내용들은 Chapter 12 의 9번째 진도에서 다룰 것이다.
전자회로 2 과정을 학습하셨습니다.
아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.

2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼
전자회로 2 커리큘럼
전자회로 2 커리큘럼입니다. 전자회로 2에 대한 간략한 설명은 아래와 같습니다. 전자회로 1에서 배웠던 능동소자(Diode, BJT, MOSFET)에 대해 학습했으며 그에 대한 다이오드 회로 및 단일 증폭기인
doctorinformationgs.tistory.com
'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 공유 결합(covalent bond), 정공(hole), 밴드갭 에너지(Bandgap Energy)- 전자회로 기초 (0) | 2022.01.22 |
|---|---|
| 피드백 회로의 불안정성 문제와 바크하우젠 조건을 알아보자 (2) | 2022.01.19 |
| 피드백 회로의 비이상적인 입출력 임피던스의 영향(Effects of non-ideal input/output impedance of feedback circuits.) (0) | 2022.01.17 |
| 전류-전류 피드백 증폭기(or 귀환, 궤환 증폭기), 병-직렬 피드백 증폭기의 임피던스를 알아보자 (0) | 2022.01.14 |
| 전류-전압 피드백 증폭기(or 귀환, 궤환 증폭기), 직-직렬 피드백 증폭기의 임피던스를 알아보자 (0) | 2022.01.12 |




댓글