본 포스팅을 하기에 앞서 저항의 값, 트랜지스터의 사이즈(W/L)이 모두 동일하다고 가정하여 풀이를 시작합니다.
이전 진도에 대한 복습
단일 출력과 차동 출력에 대해 생기는 이점과 단점에 대해 차동증폭기를 어느정도 시식을 해보았습니다.
2021.10.13 - [전공(Major)/전자회로와 아날로그 회로설계] - 단일 증폭기와 차동 증폭기의 차이점과 장단점 정리
단일 증폭기와 차동 증폭기의 차이점과 장단점 정리
이번 포스팅은 차동증폭기를 제대로 이해하는데에 앞서 에피타이져의 식으로 장단점과 단일 증폭기에 대한 차이점을 이해하도록 하기 위함과 차동증폭기 본문의 분량이 많아질 것을 우려해 해
doctorinformationgs.tistory.com
전류원이 없는 차동증폭기
일단 첫 걸음마인 전류원이 없는 차동 증폭기를 봅시다.
사진 1은 해당 구성을 보여주고 있는 회로이고 자세히 들여다보면 공통 소스 증폭기 2개가 병렬로 연결 되어있음을 확인 할 수 있습니다.
각각에 입력에는 M1과 M2의 전원을 켜기 위한 입력 Bias 전압인 즉 직류 바이어스와 어떤 정보가 들어있는 소신호가 들어오는 즉 교류 신호로 구성이 되게 됩니다.

두 개의 입력 신호가 크기가 같은 경우에 아래 식 1의 전압이득을 가지게 됩니다.

이전 포스팅에 언급이 되었지만 델타VDD는 공급 전압에서 오는 잡음을 의미하고 있습니다.
사진 1의 구조는 치명적인(Critical) 단점이 존재하게 되는데 각각의 cs의 소스 단자가 그라운드로 접지되어 있기 때문에 M1과 M2의 게이트-소스 단자에 인가되는 DC가 달라지는 경우에 M1과 M2에 드레인 전류가 달라짐으로 저항에 걸리는 전압강하가 달라지기 때문에 공통 모드 레벨(Common Mode Level)이 달라지고, gm의 값이 달라지게 됩니다.
이는 M1, M2, 드레인 저항에 생기는 부정합(Mismatch)로 인해 생길 수 있음을 암시하게 됩니다.
이 부분을 해결하기 위해 입력 트랜지스터의 드레인 전류가 입력 공통 모드 전압에 예민하지 못하게(insensitive) 유지해야합니다.
해결 방법으로는 M1과 M2 소스 단자에 전류원을 삽입함으로써 일정한 전류를 공급해줄 수 있도록 문제점을 해결할 수 있습니다. 다르게 이야기하면 ID1, ID2는 각각 M1과 M2의 게이트-소스 전압의 함수를 전류원의 게이트-소스 전압의 함수로 바뀌게 되면 M1, M2의 Vgs와 무관한 함수가 되기 때문입니다.
차동(Differential)과 공통(Common) 이게 무슨말인데?
학부 시절에는 이 두 단어에 대해서 그냥 읽고 스윽 넘어갔었는데 언제나 햇갈렸던 문제점이 있었습니다.
그래서 이 글을 읽는 분들에게 어려움을 좀 해소시켜드리고자 추가하였습니다.
사진 1에 M1, M2의 직류 전압이 인가되어 출력에 직류 출력로 구성된 출력 전압이 Vx, Vy로 같은 값이 나옴을 알 수 있었고 Vxy에서 서로 상쇄어집니다 식 1 참조
그러면 교류의 신호가 반대의 위상으로 입력되지 않고 같은 위상으로 들어오면 어떻게 될까요? 다시 말해서 Vin=Vin1=Vin2라면 출력 전압이 어떻게 나올까요?
직류로 신호가 입력이 동일하게 입력이되어 출력 Vxy의 값에서 Vx, Vy의 값이 서로 상쇄되어 지워진 것 처럼 같은 위상의 교류신호도 직류와 동일하게 지워집니다.
서로 반대되는 신호가 들어오게 되면 출력 신호는 단일 증폭기와 동일한 이득을 같지만 잡음을 지워주는 좋은 특성을 가지게 됩니다.
식 1에서 이득의 표현은(Vout)/(2Vin)
이제 단어의 어원을 살펴보도록 합시다.
차동(差動, Differential) : 한자로는 어긋날 "차", 움직일 "동" 어긋나게 움직인다 라고 생각할 수 있고, 영어로는 두 값의 차이라고 생각하시면 되겠습니다.
공통(共通, Common) : 함께 "공", 통할 "통", 함께 통한다...라 즉 같이 가는 것 또는 동상(同, 한가지"동",相, 서로 "상") 서로 한가지로 간다... 즉 같은 위상으로 간다는 의미이다. 영어로는 두 명 이상의 사람이나 집단에 공통적으로, 그것은 행해지거나 소유되거나 그들 모두가 사용한다... 라고 되어있습니다.
정리해보면 공통모드는 같은 위상으로 들어오는 직류와 같은 신호를 공통모드라고 합니다. 따라서 이 공통모드로 인가된 출력전압은 Vxy(같은 위상 신호의 출력전압)은 0이 되는게 가장 좋겠죠? 0이 아니면 M1과 M2 이 쌍(pair)이 서로 다른 전류, 전압을 할당하는 의미가 되니까요
차동 모드는 서로 반대되는 위상을 가지고 들어오는 신호를 의미하게 됩니다.
기본적인 차동 쌍(Basic Differential Pair)
자 Chapter 3 단일 증폭기에서 MOS는 전류원으로도 사용 가능하다고 말씀을 드렸습니다. 즉 ISS는 결국 전류원으로 동작하는 MOS임을 알 수 있고 이 전류원을 꼬리 전류원(Tail Current Source, 테일 전류원)로 부릅니다.
M1과 M2의 게이트-소스 전압이 같다면 각각 절반의 테일 전류를 흘릴 수 있음을 알 수 있죠.
이 테일 전류원은 전류원으로 동작하기 위해 항상 포화영역에서 동작하고 있음을 유의하시기 바랍니다.

기본적인 차동 쌍의 정성적 해석
대신호해석을 통해 차동증폭기의 동작점(또는 바이어스점)을 확인한다 대신호 해석에서는 저항, 트랜지스터 M1, M2의 사이즈가 동일하다고 가정하고 해석하게 되는데 이는 뒤에 나오는 오프셋 전압 문제를 다룰 때 도움이 되기도 한다.
정성적 해석 - 전압과 전류
같은 게이트-소스 전압(Vgs)와 같은 드레인 저항(RD)의 전압강하로 인해 인가되는 드레인-소스 전압(Vds)이 인가되는 M1, M2는 결국 같은 드레인 전류가 흐르게 됨을 알 수 있다.
그렇다면 동일하게 입력된 M1과 M2의 게이트-소스 전압이 서로 다른 값으로 바뀌게 되면 어떨까? 라는 의문점을 가져야 한다.
이런 변화를 알기 위해 Vin1-Vin2의 변화에 따른 드레인 전류의 변화를 이해해야 한다.
둘이 같다면 위에 언급했었던과 동일하게 M1과 M2의 전류가 같아야하고 전체 전류를 흐르게 하고 있는 테일 전류의 절반씩 M1과 M2가 할당하고 있음을 이야기한다.
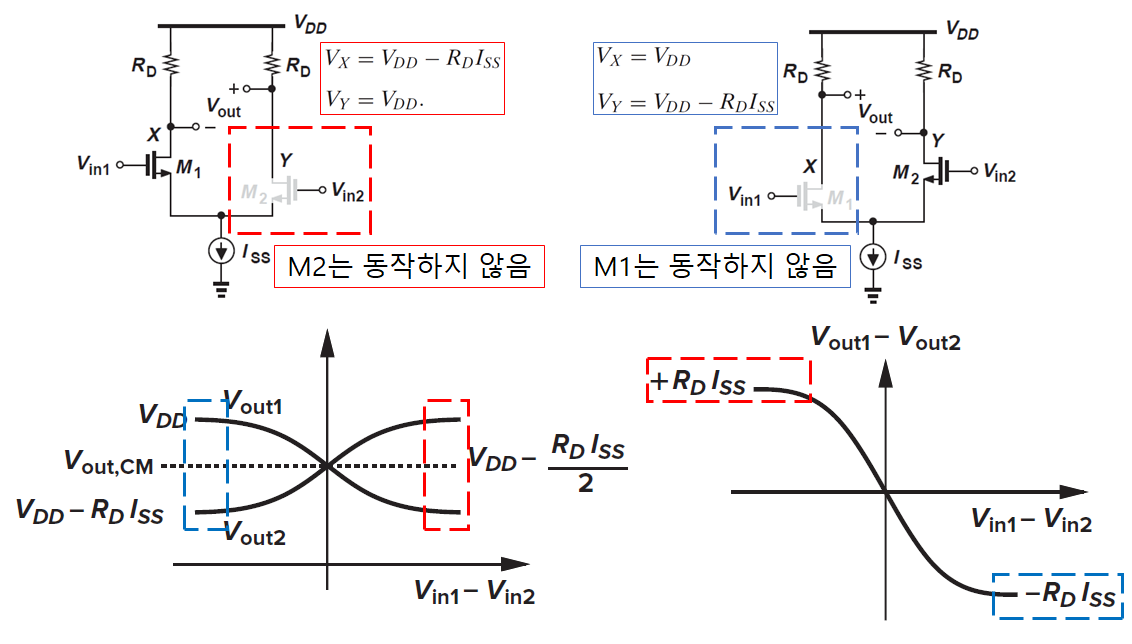
사진 2의 노드 X, Y의 전압은 아래와 식2와 같고 Vin1-Vin2 변화에 따른 전류의 변화는 사진 3으로 표현 가능하다.
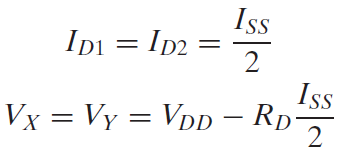

사진 3을 통해 알 수 있는점은 Vin1-Vin2 가 양의 값을 가지면 M1의 드레인 전류가 Iss의 값에 가까워짐을 알 수 있고 Vin1-Vin2가 음의 값을 가지게 되면 M2의 드레인 전류가 Iss에 가까워짐을 알 수 있다.
Vin1-Vin2가 양의 값, 음의 값이 되게 되면 사진 2 회로에서 M1, M2의 소스 단자, 사이에 있는 테일전류원과 연결된 노드(Vp)의 전압이 변하게 되는데 사진 3을 참고하면 양의 값으로 상승하면서 Iss에 도달할 쯤 회로의 동작을 보게 되면 때 M1의 소스 단자의 전압이 높아지기 때문에 노드 Vp의 전압은 0에서 M1의 소스 전압(Vs1)에 비례하게 올라가게 된다.
M2의 소스 단자의 전압이 높아짐으로 M2의 게이스-소스 단자는 문턱 전압 밑으로 떨어져 Cut off 상태가 되어버린다.
반대로 Vin1-Vin2가 음의 값이 되면 M2의 소스 단자(Vs2)의 값이 올라가기 때문에 M1이 Cut off 상태가 된다.
이에 대한 결과는 사진 4를 통해 입출력 전압 특성을 확인 할 수 있다. 하단 좌측은 Vx, Vy의 전압이고 하단 우측은 Vxy의 전압을 그린 것과 해당되는 상태의 X,Y 노드의 전압을 확인 할 수 있다.
정성적 해석 - 소신호 이득
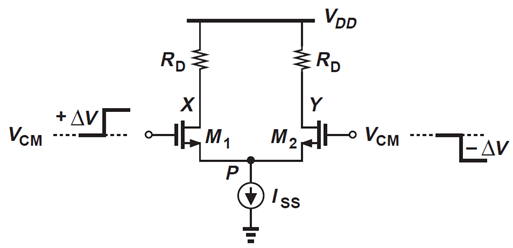
사진 5를 통해 서로 반전된 입력이 델타 V 만큼의 입력이 인가되면 식 1(앞에 했던 설명)과 동일한 과정을 거쳐 계산을 할 수 있다.
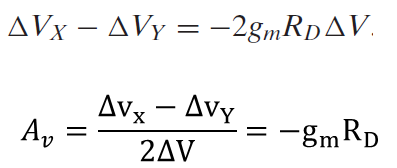
정량적인 대신호 해석과 소신호 해석
대신호 해석
대신호 해석은 정성적인 해석만 제대로 해도 다음 진도를 나가기에 문제가 없다 자세히 적은 내용은 아래 링크에서 확인 할 수 있다.
MOS 차동 증폭기 대신호 해석
정량적인 해석에 대한 내용을 담기 위한 글이다.전체적인 해석 플로우는 아래 링크 BJT 차동 증폭기 대신호 해석과 비슷하게 진행이 된다.2023.07.11 - [회로 관련 전공/회로 과정 통합 글] - 바이폴
doctorinformationgs.tistory.com
소신호 해석
소신호 해석에는 두가지 방법이 존재하는데
1. 중첩(Superposition)을 통한 소신호 해석
중첩을 통한 소신호 회로 해석은 일단 쉽고, 공정의 부정합(Mismatch)에 대한 차동 회로에 적용이 가능하지만 많은 부분을 계산해야 합니다.
2. 절반 회로 해석을 통한 소신호 해석
절반 회로 해석 같은 경우에는 중첩에 비해 훨씬 간단하지만 모든 소자들의 크기(저항, 트랜지스터의 사이즈)가 같은 회로에만 적용할 수 있습니다.
먼저 중첩부터 알아보겠습니다.
중첩을 이용한 해석
사진 2의 회로에서 중첩의 원리를 적용을 해보면 전류원은 개방회로, 전압원은 하나의 단락회로가 되는 원리인데 M1, M2의 입력전압이 2개, 테일 전류원이 있음으로 테일전류원은 개방, M2 전압원을 단락시켜 회로를 해석해본다.

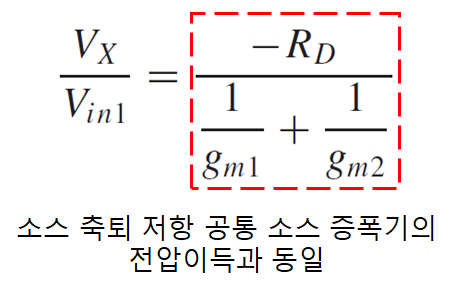
식 4을 통해 Vx에 걸린 전압이 소스 축퇴저항을 가지는 공통 소스증폭기와 유사함을 알았고 다음 단계로 Vz와 Vy에 걸린 전압을 이해해야 합니다.
노드 Vz에서 걸리는 전압은 M1이 소스 폴로워로 동작하는 것으로 보이게 됩니다. 따라서 1/gm2에 걸리는 전압강하가 Vz의 전압임을 알 수 있습니다.
이 다음이 복잡한 과정인데
Vz는 입력 전압의 절반을 공급해주는 하나의 전압원으로 볼 수 있기 때문에 M2는 입력전압이 절반이 인간된 공통 게이트로의 동작으로 볼 수 있습니다.
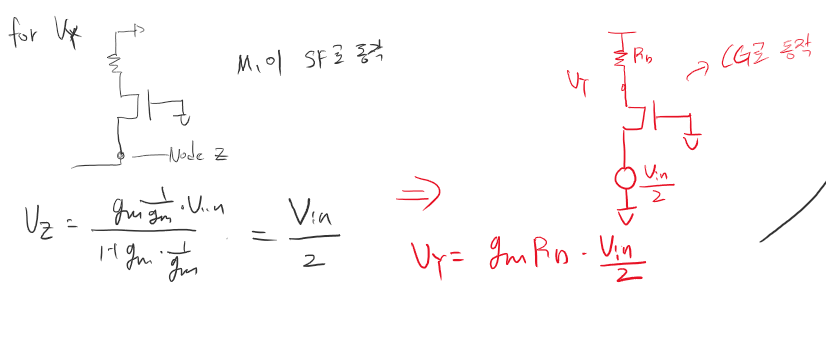
공통 게이트의 전압이득은 식 6으로 표현이 되고 M2 전압원을 단락 시킨 출력전압은 식 7로 나오게 됩니다.
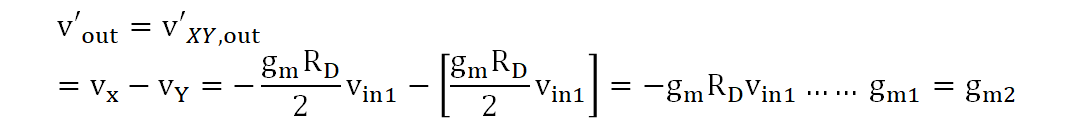
동일한 작업으로 M1의 입력 전압원을 단락시키고 M2의 반대의 위상을 가진 입력전압이 인가된 상태에서 출력전압은 식 8과 동일합니다.
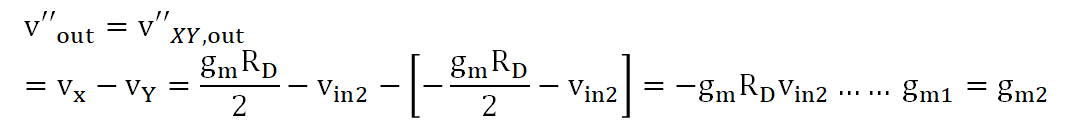
개별의 전압원을 통한 출력 전압을 식 7, 8로 구했음으로 출력 전압 성분을 더하게 되면 식9가 나오게 됩니다.
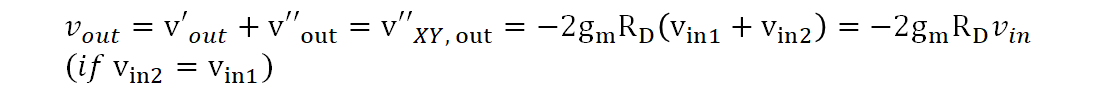
전압이득은 식 3과 동일하게 -gmRd로 나오게 됩니다.
절반회로 개념을 이용한 회로 해석
이 부분에 대한 설명은 사실 사진 3과 사진 4 사이에 있는 내용에 어느정도 설명이 되어있습니다만
그림을 더 추가해보면서 자세한 원리로 알아보도록 합시다.
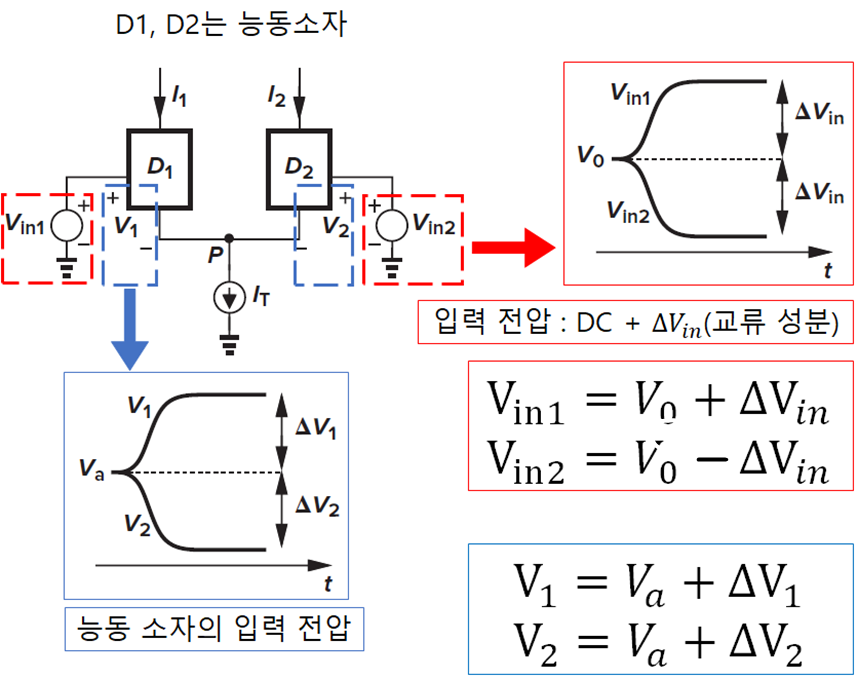
개별적인 능동소자의 특성을 고려하지 않기 위해 D1과 D2는 능동소자(BJT, MOSFET ...)을 하나의 블록박스로 그린 것입이며 Vo와 Va는 DC 레벨임을 확인 해야한다.
Vin1과 Vin2가 차동입력으로 델타 Vin 만큼의 전압이 입력이 되면 능동소자의 입력 전압도 델타V1, V2만큼의 전압이 증가 할 것입니다.
혼동하지마세요!
여기서 혼동하지 말아야 할 것이 능동소자의 입력이 델타 Vin 만큼 증가한게 아니라는 것을 유의하셔야 됩니다 전류원 It도 능동소자로 사용하기 때문에 노드 p에서 바라본 저항은 하나의 저항성분이 있고, 소스 축퇴 저항 CS 증폭기를 다시 생각해보면 전압 강하의 대부분은 노드 P에서 바라본 저항이 할당되기 때문에 V1,V2로 설명이 된 것입니다.
델타 V1, V2 만큼 전압이 움직였음으로 능동소자의 소신호 모델의 종속 전류원은 아래 사진 7처럼 변하게 됨을 알 수 있다.
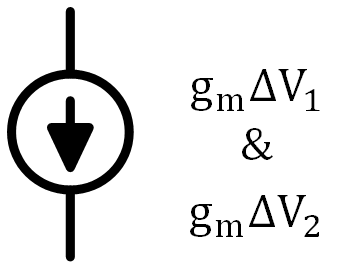
델타 V1은 양의 값, 델타 V2는 음의 값으로 차동입력이 인가 되었음으로
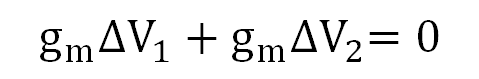
절반회로의 조건인 완전한 대칭(사이즈가 같음)회로 임으로 식 10을 정리하면
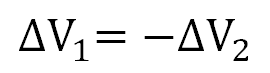
사진 6 회로에 KVL을 적용하여 계산하면 아래와 같다.(Super Mesh 사용)
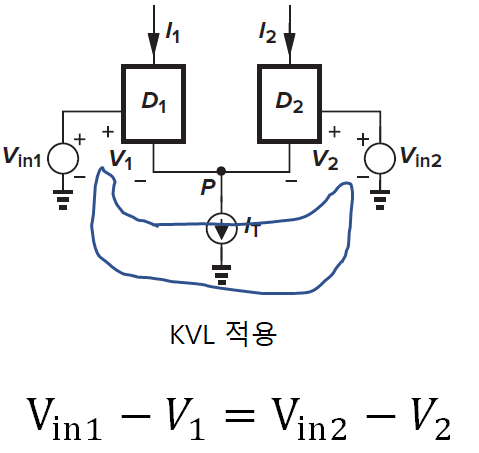
사진 6에 구해진 값을 대입해 계산하면 아래와 같다.
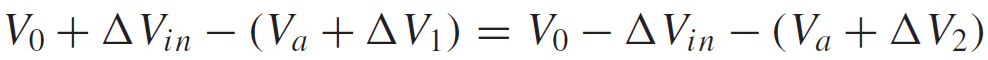
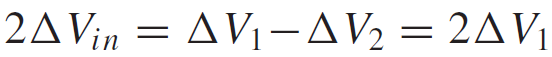
식 14에서 의미하고자 하는 것은 두 차동 입력의 변화는 각 능동소자에서 입력 전압(V1, V2)의 변화도 그대로 나타나게 되는 관계를 알고 있는 상태에서 mesh를 사용하여 개별 능동소자와 노드 P의 전압은 아래와 같다.

뭔가 어디선가 본 식임을 확인 할 수 있는데 식 12와 동일한 관계를 가지고 있다. 델타Vp는 델타 V만큼 차동으로 입력전압이 증가하게 되면 Vp의 전압의 변화는 없기 때문에 가상 접지(또는 교류 접지, ac ground, virtual ground)로 볼 수 있다.
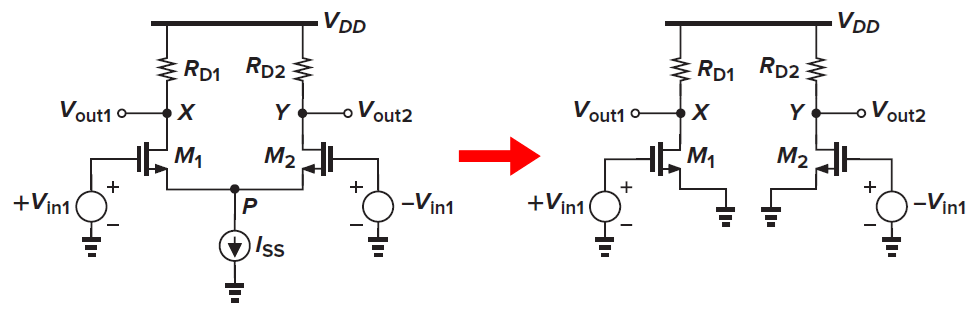
따라서 노드 Vp를 기준으로 절반으로 표현되는 회로로 표기가능하며 앞서 언급했던 전류원이 없는 차동 쌍과 동일하게 표현이 가능하고 전압이득도 동일하게 gmRD를 가지게 된다.
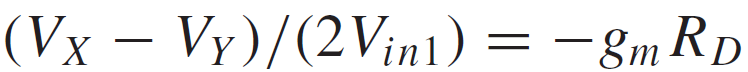
사진 9는 절반회로의 과정을 MOSFET에 적용하여 나온 결과를 보여준다.
전자회로 2 과정을 학습하셨습니다.
아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.

2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼
전자회로 2 커리큘럼
전자회로 2 커리큘럼입니다. 전자회로 2에 대한 간략한 설명은 아래와 같습니다. 전자회로 1에서 배웠던 능동소자(Diode, BJT, MOSFET)에 대해 학습했으며 그에 대한 다이오드 회로 및 단일 증폭기인
doctorinformationgs.tistory.com
'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 차동 증폭기의 공통모드 응답 (2) | 2021.10.18 |
|---|---|
| BJT의 NPN, PNP 동작과 얼리 효과(early effect) (0) | 2021.10.15 |
| 단일 증폭기와 차동 증폭기의 차이점과 장단점 정리 (0) | 2021.10.13 |
| 공통 소스 증폭기 개념과 응용 회로들을 알아보자 (4) | 2021.10.13 |
| 소신호 등가모델(Small Signal Equivalent Model)에 알아보자 (0) | 2021.10.09 |




댓글