적분기와 미분기 / op-amp 응용회로

적분기와 미분기를 들어가기 전에 우리는 시간 영역과 s 영역에서의 표현을 왜 하는지에 대해 알고 넘어가야 한다.

---

시간 영역과 주파수 영역(또는 s영역)

---

 

시간 영역(t-domain)에서의 회로해석의 계산 과정은 복잡하고 시간을 많이 잡아먹는 문제점이 생긴다.

그래서 간단하게 에너지 저장 소자의 회로 해석을 간단하게 하고자 s 영역(s-domain)에서의 회로를 해석하는 것이다.

 

그리고 관심 주파수에서는 s=jw이므로 값을 대입하고, w=2*pi*f 이니 보데선도를 통해 미분기와 적분기가 어떤 필터로도 동작하는지 알 수 있게 된다.

 

---

적분기

---

적분기는 LPF로 동작하게 되는데 식에 대한 증명과정과 주파수 응답을 통해 알아보자

 

적분기 구조

 

그림 1. 적분기의 구조

적분기는 반전 입력 단자에는 저항, 피드백 임피던스는 커패시터로 구성이 되어 있다.

 

t-domain 에서의 출력 전압

 

비반전 단자에 kcl을 통해 계산을 하게 되면 아래와 같은 결과가 나온다.

 

식 1

 

Vout에 대해 식을 정리하면 아래와 같다.

 

식 2

식 2를 통해 출력 전압은 입력 전압을 적분한 형태와 1/(RC)곱으로 나오게 됨을 알 수 있다.

 

s-domain에서의 출력 전압과 전달 함수

 

커패시터의 임피던스는 1/Cs로 표현이 가능하며 t-domain과 계산과정과 동일하게 KCL을 적용해 계산을 하게 되면 아래와 같다.

 

식 3

Vout에 대한 식과 전압 이득으로 표현한 식은 아래 식 4와 같음을 알 수 있다.

 

식4. 전압이득, 전달함수(Transfer Function)의 크기(Magnitude), 전달함수의 위상(Phase)

 

 

식 4를 통해 관심 주파수에 대해 s=jw=j*2pi*f 주파수 영역으로 표시하게 되면 주파수가 오를수록 전압이득이 떨어짐을 알 수 있고 이를 주파수 응답으로 표현하게 되면 아래 그림과 같이 표현 가능하다

 

그림 2. 적분기의 주파수 응답

 

 

우리는 위 주파수 응답을 통해 알아야 하는 한가지 사실이 있다.

 

낮은 주파수 즉 DC(0 Hz를 dc라고 표현)와 낮은 주파수에서 엄청 높은 전압이득이 나옴을 알 수 있고 이는 op-amp가 선형 구간 밖에서 동작함을 알아야 한다.

 

따라서 주파수가 dc 일 때 연산 증폭기(op-amp)가 개방 루프로 동작하며, 커패시터가 개방 회로가 되기 때문에 직류에서는 부귀환이 없다는 것을 인지해야 한다.

 

따라서 부귀환 회로를 만들어주기 위해 커패시터와 피드백 저항과의 병렬로 만들어 주게 되면 직류에서도 전류의 경로가 Rf를 통해 흐르기 때문에 반전 증폭기와 동일하게 동작할 것을 알 수 있다.

 

피드백 저항을 연결한 적분기에서의 전달함수는 아래와 같이 표현 가능하다

 

 

그림 3. DC에서의 문제점을 보완하기 위한 적분기와 식 5

 

---

미분기

---

사진 4. 미분기

 

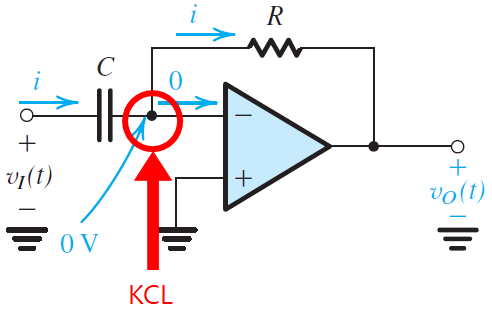
미분기는 입력 임피던스에 커패시터, 피드백 임피던스에는 저항을 연결한 구조로 사용하게 됩니다. 추가적으로 적분기는 LPF에 동작하는 반면에 미분기는 HPF로 동작하게 된다.

 

t-domain 에서의 출력 전압

 

적분기와 동일한 계산 과정인 반전 단자에 kcl을 적용하여 나오는 결과는 아래와 같다.

 

식 6

 

위 식을 통해 출력 전압은 입력 전압을 미분한 형태로 나오기 때문에 미분기라 불리는 것을 알 수 있습니다.

 

s-domain 에서의 출력 전압

 

s-domain에서의 회로 해석도 적분기와 동일하게 구해지며 전압이득은 아래와 같다.

 

식 7

 

관심 주파수에서의 s=jw이므로 이에 대한 주파수 응답을 그려보면 아래와 같이 나온다

 

그림 5. 미분기의 주파수 응답

 

---

감사의 글

 
소정의 지식을 쌓는데에 도움이 되셨다면 광고 클릭을 하여 불쌍한 대학원 노예에게 10원의 기부를 부탁드립니다.

---