이 글은 다섯번째 진도입니다.
증폭기와 감지와 반송 부분의 개념을 익히지 않으셨다면 아래 링크에 있는 두번째, 세번째 진도를 읽어주시기 바랍니다.
2021.12.28 - [전공(Major)/전자회로와 아날로그 회로설계] - 증폭기의 형태(Types of Amplifier)
증폭기의 형태(Types of Amplifier)
이 글은 증폭기에 대한 형태를 알 수 있고, 회로를 해석하는데에 있어 초심자들에게 유익할 수 있습니다. 그리고 해당 포스팅은 피드백 회로관련 글의 두번째 포스팅입니다. 이전 글 2021.12.24 - [
doctorinformationgs.tistory.com
2021.12.30 - [전공(Major)/전자회로와 아날로그 회로설계] - 피드백 회로 신호의 감지와 반송 그리고 피드백의 극성
피드백 회로 신호의 감지와 반송 그리고 피드백의 극성
이 글은 세번째 진도입니다. 이전글 2021.12.24 - [전공(Major)/전자회로와 아날로그 회로설계] - 귀환 시스템(Feedback System, 피드백 시스템)과 루프 이득(Loop Gain)에 대해 알아보자 귀환 시스템(Feedback Sy.
doctorinformationgs.tistory.com
병렬(또는 직렬) -병렬(또는 직렬),
전압-전류 귀환 이름에 대해 정확히 짚고가보자
전자회로의 서적에 따라 피드백 단원에서 각각 증폭기 형태에 따라 이름을 정하는 것에 통일성이 없음을 알 수 있다.
저도 이 단원을 학습할 때 무엇을 의미하는가에 대해 곰곰히 생각해본 시간의 비중이 많이 할당됨을 알았었죠.
어떤 연결을 표현한 경우
말 그대로 어떤 연결을 표현한 경우가 되겠다. 예를 들어서 직-직렬(Series-Series), 직-병렬(Series-Shunt), 병-직렬(Shunt-Series), 병-병렬(Shunt-Shunt) 과 같은 경우다.
병(또는 직)-병렬(또는 병렬)에서 앞에 "병"은 입력 단자와 피드백 네트워크의 출력과 병렬로 연결됨을 의미하고, 뒤에 병렬은 회로의 출력과 피드백 네트워크의 입력과 병렬로 연결됨을 의미한다.
사실 피드백 챕터에서는 다양한 이름들이 쓰이고 있다.
병-병렬 피드백 증폭기, 병-병렬 귀환 증폭기, 병-병렬 궤환 증폭기, 병-병렬 귀환, 병-병렬 궤환, 병-병렬 피드백, 전압-전류 귀환, 전압-전류 궤환, 전압-전류 피드백, 전압-전류 귀환 증폭기, 전압-전류 궤환 증폭기 등등등.... 하 복잡해
전압 또는 전류 즉 어떤 에너지의 양으로 표현한 경우
전압 또는 전류로 표현한 경우는 피드백 네트워크가 중심이 되는 것을 표현으로 두고 있다.
예를 들어서 전압-전압, 전압-전류, 전류-전압, 전류-전류 와 같은 경우이다.
전압-전류로 예를 들면 피드백 네트워크의 입력이 전압을 받는다는 것(Sense, 감지)이고 피드백 네트워크의 출력을 전류로 보낸다는(Return, 반송) 의미가 된다. 다시 말하게 되면 회로의 입력이 전류로 입력이되고, 출력을 전압을 내보낸다는 것으로 이해할 수 있다.
다시 이번 포스팅의 진도로 돌아가보자
피드백 단원에서 이전 진도의 복습
트랜스임피던스를 피드백 시스템으로 표현하자면?(첫번째, 두번째 진도에 해당)
전압-전류 피드백 시스템은 입력에 전류가 입력이 되고, 출력으로 전압이 나옴으로써 출력을 입력으로 나누었을 때 관계는 임피던스에 해당이 된다. 따라서 적은 전류로 큰 출력 전압을 만들 수있다면 높은 저항으로 표현할 수 있는 것이다.
이와 같은 관계를 TransImpedance(트랜스임피던스)라고 부른다

전압을 감지하고 전류를 반송하는 방법(두번째 진도, 세번째 진도에 해당)
전압을 감지하기 위해서는 이상적으로 무한대인 임피던스, 전류를 반송하기 위해서는 전류원으로 동작해야 하니 무한대의 임피던스를 갖는다. (그림 1 참고)
에러(E)는 회로 상에서 어떻게 구현되는가?(세번째 진도에 해당)
세 전류가 만나는 노드에서 KCL을 적용하면 그림 1과 같은 수식을 얻을 수 있다.

폐루프 이득(Closed-Loop Gain)은? (첫번째 진도에 해당)
그림 1을 통해 폐루프 이득을 아래와 같이 구할 수 있다. (그림 1을 캡쳐해서 보는 것이 유용)
에러 전류는 입력 신호와 반송 신호의 차임으로 다음과 같다.

반송 신호 즉 반송 전류는 귀환율(K)와 출력 전압이 피드백 네트워크의 입력임으로 아래와 같이 표현 가능하다.

트랜스임피던스의 출력은 입력 전류를 받아 출력 전압으로 나타내기 때문에 아래와 같다.
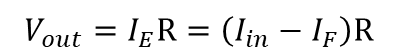
식 2를 식 3에 대입하여 트랜스임피던스의 형태(V/I)로 표현하면 아래와 같다.

이전 포스팅과 다르게 이해를 돕기 위한 문제는 마지막에 풀도록 하고 입출력 임피던스를 알아보자
입출력 임피던스
입력 임피던스
전압-전압 증폭기와 다르게 입력 임피던스는 트랜스임피던스와 직렬로 연결되어 있다. 이는 트랜스임피던스의 순방향 시스템이 전류를 감지하기 때문에 낮은 임피던스를 가지기 때문이다.
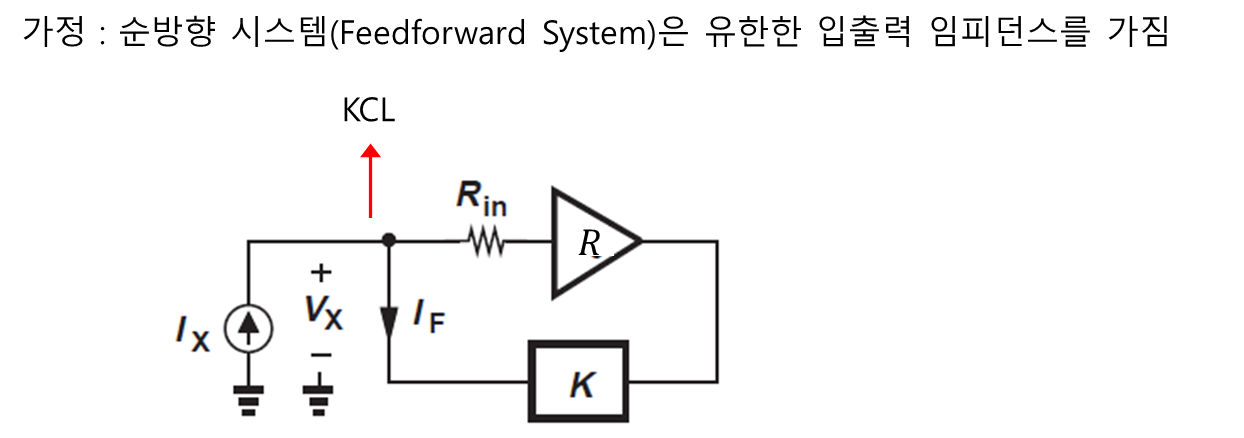
KCL을 적용해본다.
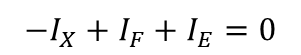
에러 전류는 순방향 시스템의 내부전압과 Vx를 통해 얻을 수 있다. 식 5를 다시 표현하면
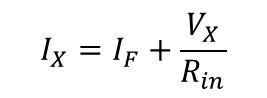
식 6을 통해 트랜스 임피던스의 입력이 Vx/Rin 임을 알았고 입력을 통한 출력은 에러 전류(I_E)가 입력으로 들어와 출력은 식 3과 비교했을 때 입력 전류가 Ix인 것만 참고하면 동일하게 나옴을 알 수 있다.
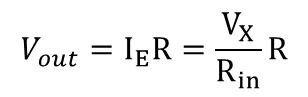
출력 전압이 다시 피드백 네트워크로 들어감으로 피드백 전류는 아래와 같이 알 수 있다.
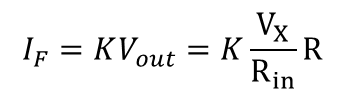
식 5에서 피드백 전류와 에러 전류를 넣어보면 다음과 같이 수정할 수 있다.
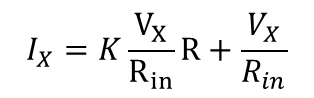
식 9를 통해 입력 임피던스의 형태(피드백 입력 임피던스)로 표현하면
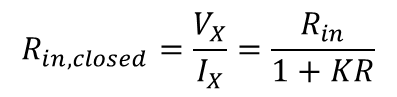
순방향 증폭기는 전류를 감지하기 위해 낮은 입력 임피던스(Rin)를 피드백 네트워크를 가짐으로써 (1+KR)만큼 더 낮춰주게 된다.
출력 임피던스
출력 임피던스를 구하기 위해서 입력을 개방(전류원이기 때문에)하고 노드에 KCL을 적용함으로써 답을 얻을 수 있다.
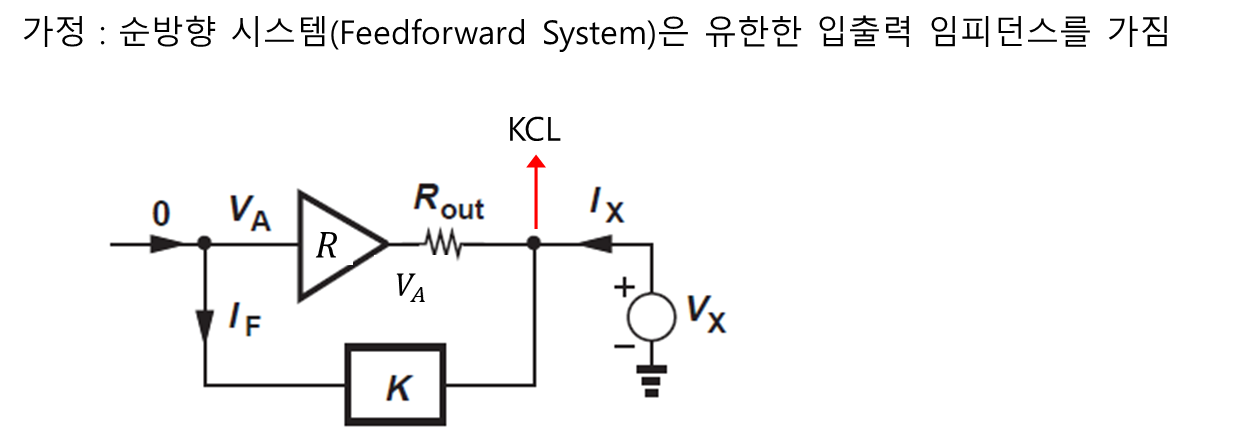
먼저 피드백 전류를 알기 위해서는 피드백 네트워크의 입력이 Vx로 입력이 됨을 알 수 있다. 따라서 피드백 전류와 에러 전압은 아래와 같다.
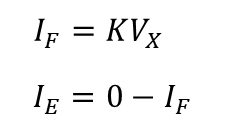
이에따라 순방향 시스템에서의 출력은 Va의 출력 전압을 만들게 된다. 출력 전압은 아래와 같다.
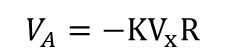
KCL을 적용하여 나온 결과는 아래와 같다(피드백 네트워크로 가는 전류는 피드백 네트워크가 무한대의 임피던스를 가지기 때문에 0이다)
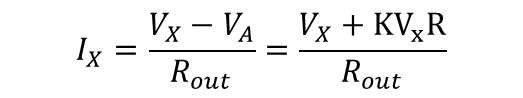
식 11을 정리하여 전압-전류 피드백의 출력 임피던스는 아래와 같다.
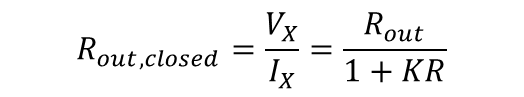
순방향 시스템은 출력 임피던스는 (1+KR)만큼 더 낮아짐을 알 수 있다.
전압-전류 귀환의 실제 회로 예
세번째 진도에서 트랜지스터를 통한 전압-전류 귀환을 맛보기로 알게 되었습니다.
아래 회로를 통해 피드백 저항을 통한 전압-전류 귀환을 알아보도록 한다.
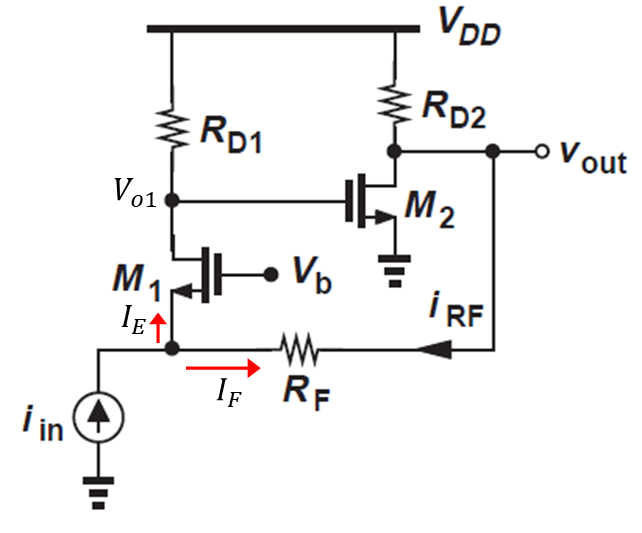
이 회로는 부귀환일까? 정귀환일까?
(Iin에는 내부 저항이 있음을 알고 있다. 따라서 출력에 KCL을 적용했을 때의 변화를 보면된다. 이 부분에 대해 모르겠다면 이번 포스팅 상단에 있는 세번째 진도 마지막 부분을 읽고와야한다.)
++ Notation을 확인하라 I는 대신호 전류, i는 소신호 전류이다.
Iin을 증가시켜보면 M1 소스에 있는 전압도 증가할 것이고, M1의 드레인 전류가 감소하기 때문에 Vo1은 증가한다. 증가된 전압이 M2 게이트에 올라감으로써 M2의 Vout은 감소할 것이고. 피드백 전류(I_F)도 증가할 것이다.
에러 전류에 있는 노드에서 KCL을 적용해보면
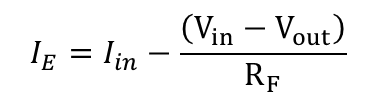
식 15에서 I_in이 증가하면, 출력전압은 감소하기 때문에 피드백 전류도 증가한다 따라서 증가된 신호를 방해하기 때문에 부귀환이다.
개루프이득(Open-Loop Gain)을 구해보자
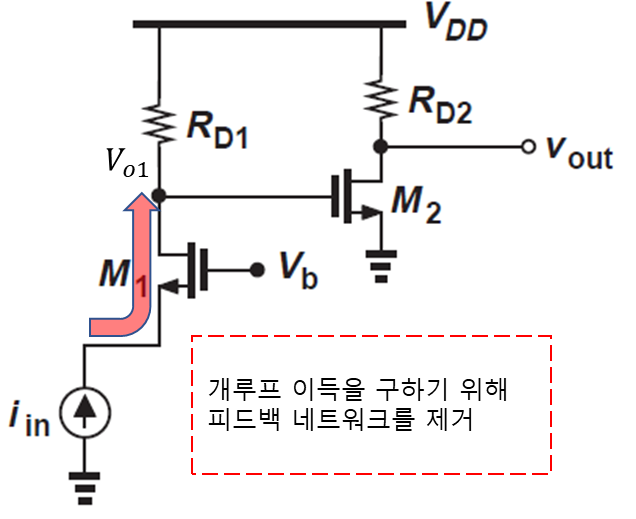
개루프 이득을 구하기 위해 피드백 네트워크를 제거하고 소신호 이득을 구하게 되면 M1의 트랜스임피던스는 아래와 같다. (입력이 전류, 출력이 전압)
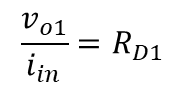
M1의 출력 전압이 M2의 입력으로 들어감으로 M2는 -gm2RD2 즉 CS의 증폭기 출력으로 나오게 된다.
따라서 개루프 이득은 아래와 같다.
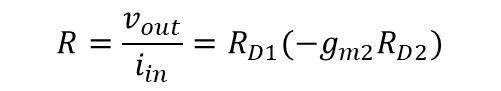
식 17에서 RF와 병렬로 연결되어있는게 정답이지만, 전압을 감지하기 위해서는 아주 높은 저항이 쓰임을 알 수 있기 때문에 생략 가능하다.
폐루프 이득(Closed-Loop gain)을 알아보자
먼저 표기를 생각해보자.
그림 5에서 i_RF의 전류의 방향은 i_F와 반대 방향임을 알 수 있다.
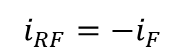
M1 소스에서 바라보는 임피던스는 1/gm1임을 알 수 있다. 따라서 아래 그림 6처럼 회로의 일부로 표현 할 수 있다.
(이해가 가지 않는다면 하단에 링크를 걸어놓은 Cascode 전류거울을 참고)
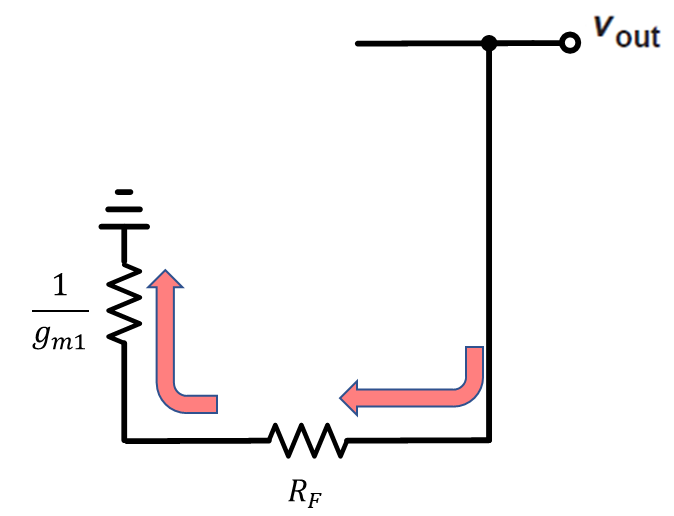
따라서 식 19와 같이 식을 표현할 수 있다.
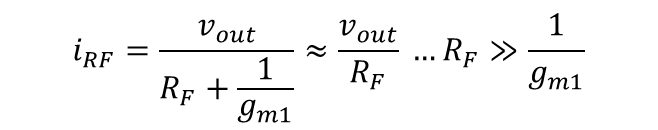
R_F는 매우 큰 저항이니 식 19와 같이 근사 할 수 있다.
식 4와 같이 계산을 하려면 식 19를 통해 K를 계산하여야 한다.
그림 1 전압-전류 피드백 시스템에서 K=I_F/Vout 임을 알 수 있는데 아래와 같이 조건들을 고려해서 풀면된다.

식 4에 구했던 값들을 대입하면 아래와 같다.
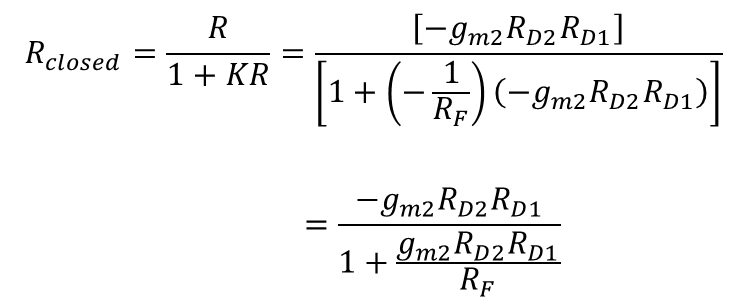
입출력 임피던스를 알아보자
입력 임피던스
유한한 내부저항(Rin)은 1/gm1 이므로 아래와 같다.
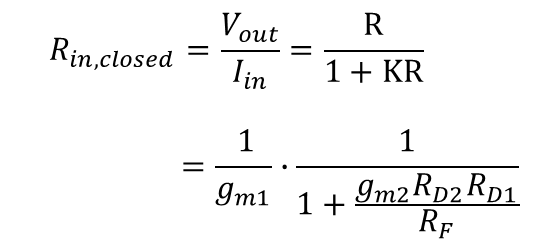
출력 임피던스
유한한 내부저항(Rout)은 RD2 이므로 아래와 같다.
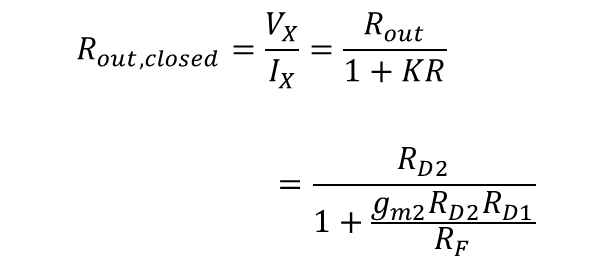
Cascode 전류거울
2021.11.04 - [전공(Major)/전자회로와 아날로그 회로설계] - 캐스코드 전류 거울(Cascode Current Mirror)
캐스코드 전류 거울(Cascode Current Mirror)
이 글은 학부 4학년 또는 대학원 진도임으로 다소 어려울 수 있음 기존에 전자회로에서는 채널 길이 변조(Channel Length Modulation)을 고려하지 않고 설계를 하였으나 드레인 전류는 Vgs와 Vds의 함수이
doctorinformationgs.tistory.com

'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 전류-전류 피드백 증폭기(or 귀환, 궤환 증폭기), 병-직렬 피드백 증폭기의 임피던스를 알아보자 (0) | 2022.01.14 |
|---|---|
| 전류-전압 피드백 증폭기(or 귀환, 궤환 증폭기), 직-직렬 피드백 증폭기의 임피던스를 알아보자 (0) | 2022.01.12 |
| 전압-전압 피드백 증폭기(or 귀환, 궤환), 직-병렬 피드백 증폭기의 임피던스를 알아보자 (0) | 2021.12.31 |
| 피드백 회로 신호의 감지와 반송 그리고 피드백의 극성 (2) | 2021.12.30 |
| 증폭기의 형태(Types of Amplifier) 또는 증폭기의 종류 (0) | 2021.12.28 |




댓글