피드백 회로의 위상 마진(Phase Margin)

피드백회로 단원의 11번째 진도이자 및 주파수 보상 챕터의 네번째 진도이다.

(이 글은 상급 내용도 다루고 있다. 이 둘의 내용에 대해서 구분선을 놓을테니 어려우면 읽지 않아도 좋다)

---

내용이 어렵다면 아래 내용을 읽어보시길 바랍니다.

2022.01.24 - [전공(Major)/전자회로와 아날로그 회로설계] - 피드백 회로의 안정조건(Stability Condition of Feedback circuit)

피드백 회로의 안정조건(Stability Condition of Feedback circuit)

---

이전 진도를 간략하게 보도록 하자

 

아래 복습 식 1과 같이 바크하우젠 조건을 만족 시키면 피드백 시스템은 발진하게 된다.

 

복습 식 1

 

이를 이득 교차 주파수와 위상 교차 주파수를 통해 보면 복습 그림 1과 같다.

 

복습 그림 1. 

 

따라서 발진(Oscillation)을 피하기 위해 이득 교차 주파수가(ωGX)가 위상 교차 주파수(ωPX)보다 낮아야 함을 알 수 있다.

 

복습 식 2

 

위 두 위상이 얼마나 많이 차이나야 하는가에 대답은 위상 마진(Phase Margin)에서 설명하도록 한다.

 

---

위상 마진(or 위상 여유, Phase Margin, PM)

---

 

위상 마진에 대한 개념을 이해하기 위해서는 아래 그림 2를 통해 예시를 보도록 하자.

 

 

그림 2. 이득교차 주파수와 위상 교차 주파수의 차이에 따른 안정성을 보여주는 예시

 

그림 2는 두 주파수(이득 교차와 위상 교차)의 차이를 보여주고 있는데 이 둘의 차이는 양방향 화살표를 통해 보여주고 있다.

 

식 2에서 두 주파수(이득 교차와 위상 교차)의 차이가 그리 크지 않는 경우 오랫동안 진동하다가 나중에 안정적인 상태로 간다는 것을 알려주며 차이가 큰 경우 피드백 시스템이 안정적으로 동작하고 있음을 보여준다.

 

두 주파수의 차이는 피드백 시스템의 안정성의 양을 알려주는 척도이며 이를 위상 마진(or 위상 여유, Phase Margin, PM)이라 부른다.

 

해당 식은 아래 식 1과 같이 표현 가능하다.

 

식 1

---

조금 더 어려운 내용(생략 가능)

 

안정성을 유지하기 위해 루프 이득의 위상은 -180도를 넘기 전에 루프이득은 1로 떨어져 함을 그림 2에서 보았다.

ωGX에서 위상이 -175° 인 극한 상황을 보도록 한다.

 

폐루프 시스템은 ωGX에서 KH(jω1)=1e^(-j175°) 이다 따라서 아래와 같이 쓸 수 있다.

 

식 2

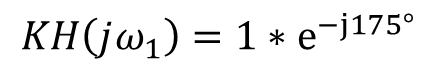
폐루프 시스템은 아래와 같이 계산이 가능하다(ωGX, 오일러 참고)

 

식 3

 

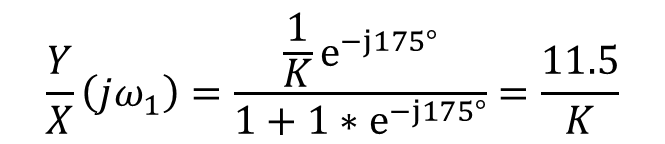
이는 그림 3과 같이 표현이 가능하다

 

그림 3.폐루프 시스템의 주파수 응답과 시간 응답

 

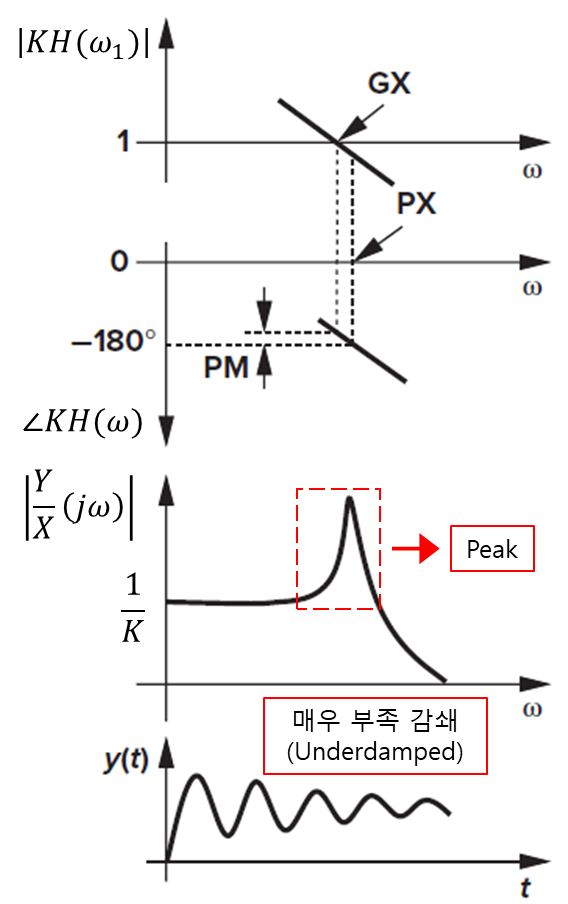
그림 3을 통해 폐루프 시스템의 주파수 응답은 ω=ω1에서 날카로운 피크를 가지는데 이는 폐루프 시스템은 발진에 가깝게 되며 time-domain에서 출력 y(t)에서는 underdamped의 형태를 가짐을 알 수 있다.

 

 

따라서 그림 2에서 Margin을 충분하게 가져야 함을 다시 상기할 수 있다.

 

조금 어려운 내용 부분 끝

---

어느정도의 여유가 적합한지에 대해 알아보도록 한다.

 

식 1을 통해 PM은 45° 60° 90° 에 대한 그래프를 알 수 있다.

 

그림 4. 위상 마진에 따른 폐루프 시스템의 시간 응답

 

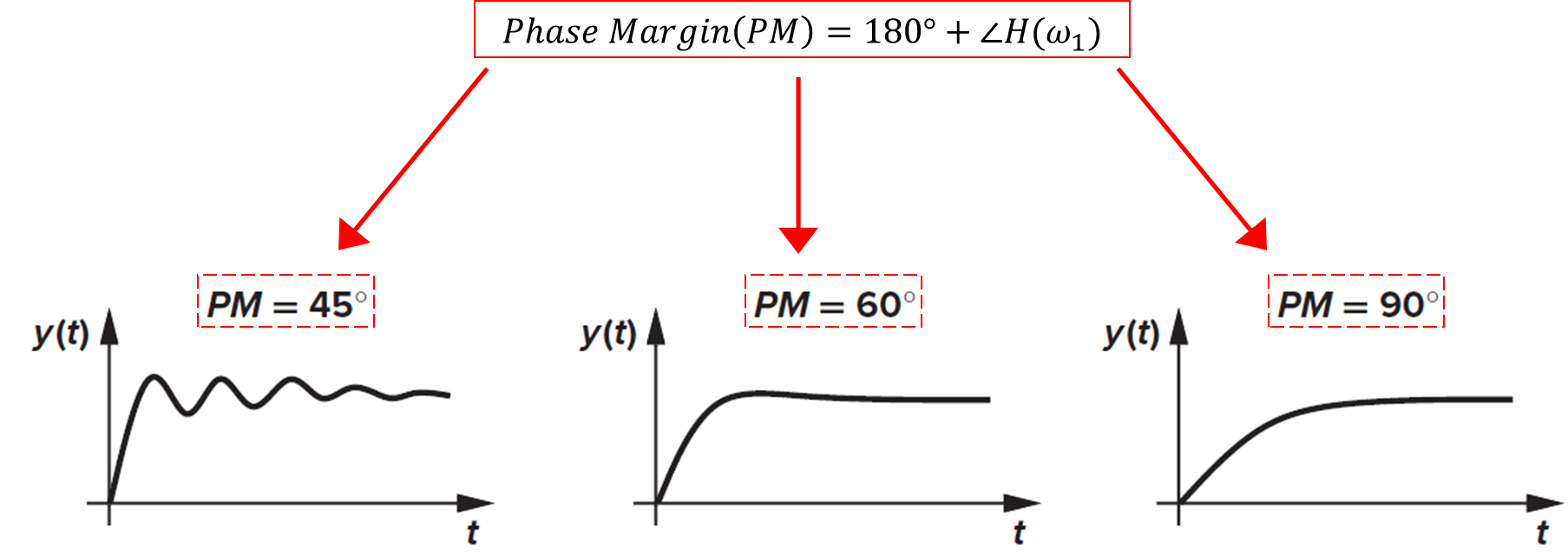
PM이 높을 수록 안정적인 값을 가지지만 PM이 60° 를 일반적인 최적의 값으로 보며 PM이 커질수록 시간 응답이 늦어짐을 확인하자.

(조금 더 어렵게 이해하고 싶으면 식 3의 방법으로 계산해보면 알 수 있다.)

 

---

(조금 더 어려운 내용 생략 가능)

PM과 UGF의 관계 및 1 Stage and 2 Stage amp 예시

---

UGF는 Unity Gain Freq이며 이득이 1이 되는 지점이다 따라서 UGF=ω1 이며, 편의상 UGF라 적는다.

 

이중 극점 시스템에서의 위상 마진

 

이중 극점 시스템에서 전달함수는 아래와 같다.

 

식 4

 

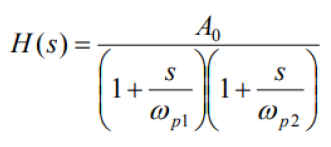
식 4에서 ωp1<<ωp2일 일 때 충분히 넓게 극점들이 분리된다. 따라서

 

1) UGF=ωp2 (in rad/s) 일 때 위상 마진은 45° 이다.

 

식 1을 통해 계산하게 되면 두번째 극점에서 위상은 -135° 이기 때문이다.

 

2) UGF=ωp2/(sqrt(3)) (in rad/s) 일 때 위상 마진은 60° 이다. 

 

식 1을 통해 계산하게 되면 위상 마진이 60°  이면 ωGX는 120°  임을 알 수 있다.

 

식 4에서 첫번째 극점에서 -90° 의 변화가 생겼고, 두번째 극점에서 -30° 떨어질 때 임을 알 수 있는데 이를 복소수로 표현하게 되면 아래와 같다.

 

그림 5. 복소수 표현

 

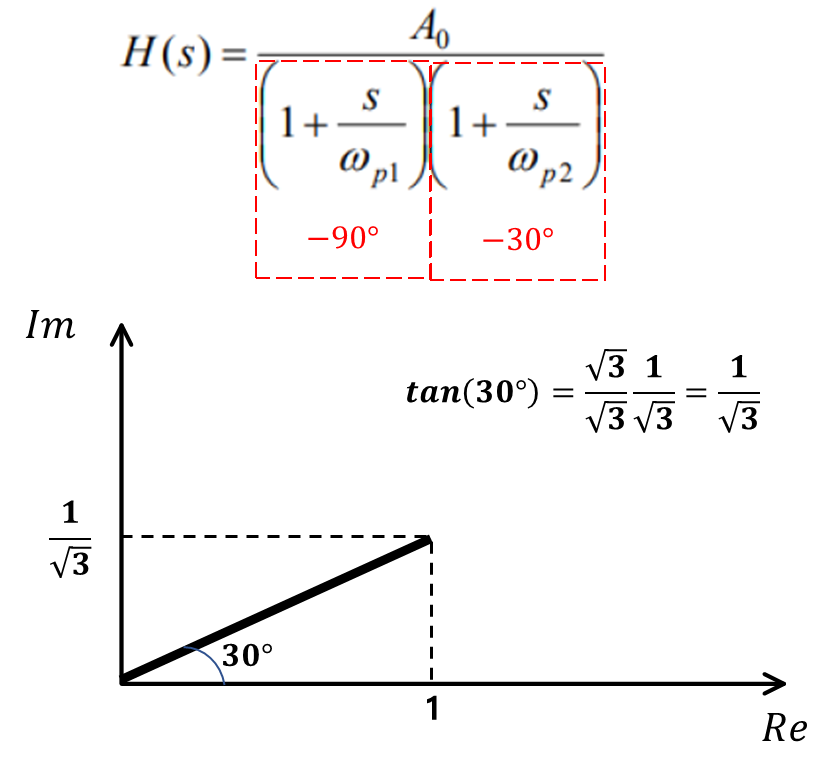
따라서 UGF는 아래와 같다.

 

식 5

 

 

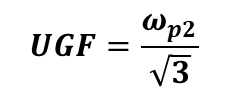
1 & 2 Stage amp 예시

 

아래 그림을 보도록 하자

그림 6. 1 Stage CS amp

 

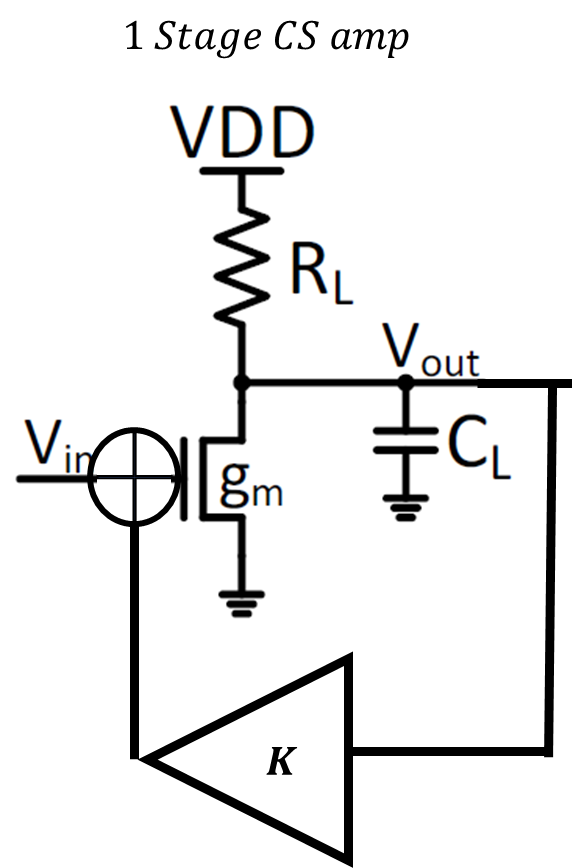
1단 증폭기의 루프이득은 아래와 같다.

 

식 6

 

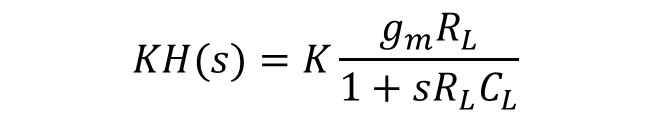
UGF는 아래와 같다.

 

식 7

 

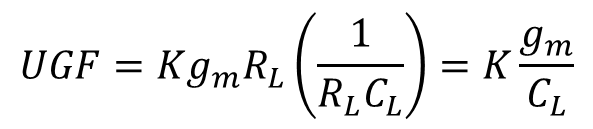
다음 그림은 2단 증폭기 이다.

 

그림 7. 2 Stage CS amp

 

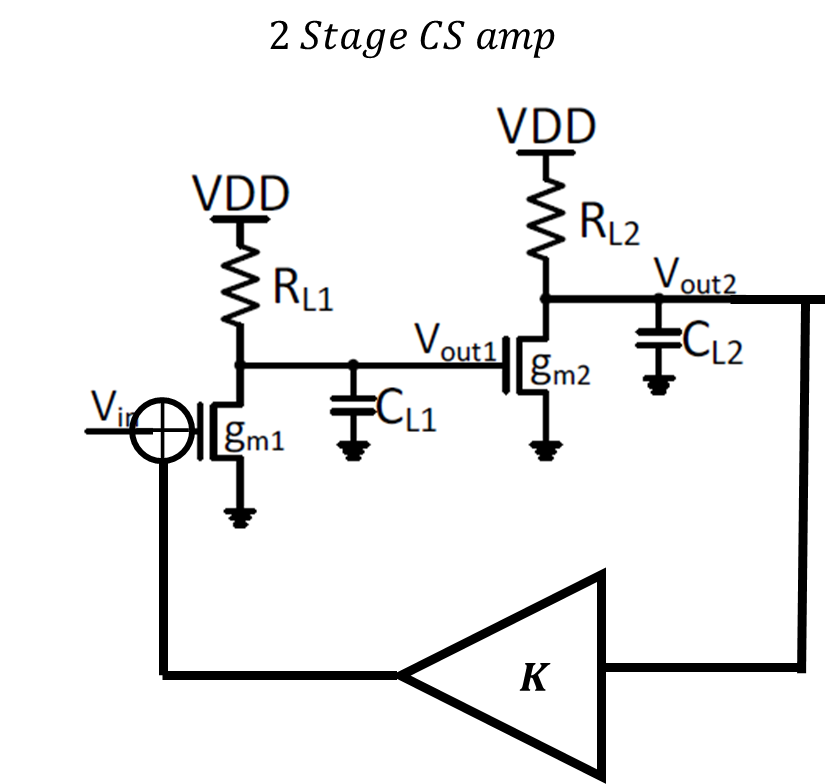
Bode Plot을 해보면 아래 그림과 같음을 알 수 있다.

 

그림 8. 2 Stage CS amp의 주파수 응답

 

UGF는 저주파 이득과 극점1(ωp1)임을 알 수 있으며 UGF는 아래와 같다.

 

식 8

 

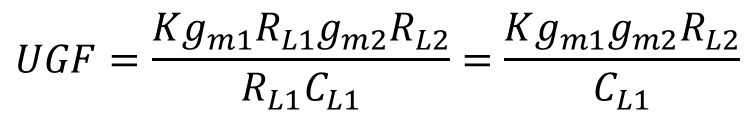
위에서 언급했듯이 만약 

 

1) UGF=ωp2 (in rad/s) 일 때 위상 마진은 45° 인 경우

 

부하 캐패시터인(CL1)을 고려하고UGF=ωp2 이므로 다음과 같이 쓸 수 있다.

 

식 9

 

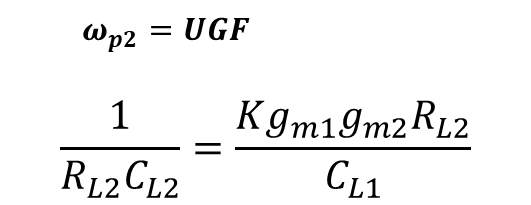
따라서 CL1 값은 아래와 같이 정할 수 있다.

 

식 10

 

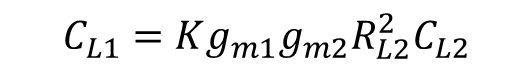
2) UGF=ωp2/(sqrt(3)) (in rad/s) 일 때 위상 마진은 60° 인 경우

 

이는 그림 5에서 이미 언급되었으므로 아래와 같이 됨을 알 수 있다.

 

식 11

 

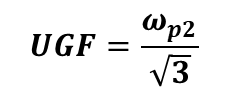
식 11을 통해 PM=60 인경우 부하 커패시터(CL1)은 아래와 같다.

 

식 12

 

 

---

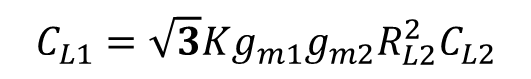
전자회로 2 과정을 학습하셨습니다.

아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.

2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼

전자회로 2 커리큘럼

---