이 글은 매우 중요한 부분이자 기초 반도체 물리의 세번째 진도입니다.
전자회로를 해석하는데에 있어 해당 내용은 MOSFET 물리까지 배우는데 계속 나오게 된다.
이전 진도
2022.01.25 - [전공(Major)/전자회로와 아날로그 회로설계] - 진성(고유,intrinsic) 반도체와 외부(외인성, extrinsic) 반도체에 대해 알아보자
진성(고유,intrinsic) 반도체와 외부(외인성, extrinsic) 반도체에 대해 알아보자
전자회로 1과정에서 기초반도체 물리는 중요한 것들만 집고 넘어가겠다. 이 글은 기초 반도체 물리의 두번째 진도이다. 이전 진도 2022.01.22 - [전공(Major)/전자회로와 아날로그 회로설계] - 공유 결
doctorinformationgs.tistory.com
이전 진도와 기초 물리 복습
이전 진도에서는 캐리어(전자, 정공)와 도핑(dopant)의 개념을 알았으며 기초 물리에 대해 간단하게 짚고 넘어가자
1. 전압(또는 전위차 Voltage)는 전기장을 E 를 거리에 대해 적분하여 음에 값을 취한 것과 같다.

2. 전류 방향에 대한 개념은 양의 전하를 양의 전압에서 음의 전압으로 이동시킨 것과 같다. 즉 전자가 A 지점에서 B로 이동할 때 전류는 B->A의 방향을 가짐
드리프트(Drift)
먼저 드리프트의 사전적 의미를 보자
drift : (서서히 일어나는) 이동
어떤 이동이 있다는 것을 의미하게 되는데 무엇을 이동을 시킬까?
바로 전하 캐리어를 이동시키게 하는 것을 의미하게 된다. 반도체 물리에서 전기장은 물질에서 전하 캐리어를 가속시켜, 한쪽에서 다른쪽으로 이동시킨다. 따라서 전기장(E)에 의한 전하 캐리어의 이동을 드리프트(drift)라고 부른다.
이해를 돕기 위해 그림 1을 보도록 하자

그림 1을 유심히 보게 되면 전하 캐리어(동그라미 점)는 전기장에 의해 가속되면서 수정(crystal)의 원자와 충돌하는 과정을 거쳐 반대편으로 도착해 배터리에 들어간다.
정리하자면 전기장(E)에 의한 가속과 수정에서의 충돌은 캐리어에 일정한 속도(v)를 주는데 속도는 전기장(E)에 비례하는 관계를 가진다.
속도에 대해 식을 쓰면 아래와 같다.

여기서 μ는 이동도(mobility)이며 n형, p형에 따라 이동도는 달라지게 된다.

식 3에서의 dot은 내적을 의미한다.
전자는 전기장과 반대로 움직이기 때문에 속도 벡터(vector)로 나타낼 수 있는데 식 3을 벡터로 표현하면 아래와 같다.

식 4에서 v의 아랫첨자는 electron(e)과 hole(h)을 의미한다. 또한 전류를 표현할 때는 n형 반도체는 양의 값, p형 반도체는 음의 값이 나타난다는 것을 의미하기도 한다.
(이는 이전 진도에서 자유 전자의 이동방향, 정공의 이동 방향을 생각하면 이해하기 더 쉽다)
다음 내용으로 전류의 계산에 대해 알아보도록 하자.
전류 밀도(Current Density)
전류 밀도의 결과식을 먼저 보도록 한다.
전자회로는 반도체가 가지는 특성을 통해 회로 해석을 가지기 때문에 자세한 공식의 증명과정은 고체전자물리를 하게 되면 따로 수록하도록 한다.
그림 1과 같은 막대기는 폭(Width), 길이(Length), 높이(Height)를 고려하고, 속도 v [m/s]의 전자가 이동할 때의 전류 밀도는 아래와 같다.
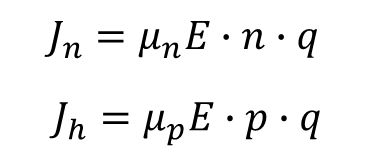
식 4-5 에서 Jn 은 자유 전자의 전류밀도, Jp는 정공의 전류 밀도이다. n과 p는 자유 전자와 정공의 "밀도", q는 기본 전하이다
(틀리면 지적해주길 바란다.)
전류(Current, I)는 실제로 전류 밀도를 나타내며 (+)(-)의 부호는 적당히 추가 될 수 있음을 알길 바란다.
전자와 정공이 함께 있을 때는 아래와 같이 표현이 가능하다.
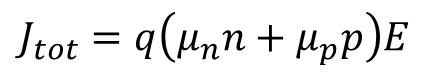
식 6에서 tot는 total을 의미하고, 반도체에서의 드리프트 현상에서 발생하는 전류 밀도는 자유 전자의 전류밀도와 정공의 전류 밀도와 합한 결과와 전기장(E)이 가해진 것과 같다는 것을 알 수 있다.
확산(Diffusion)
확산(Diffusion)에 대해 가장 이해하기 쉬운 예는 어느 책, 어떤 사람이 거의 동일하게 설명을 한다.
예를 들어 우리가 어떤 물이 찬 세숫대야에 코피 한방울 흘렸다거나 잉크 한방울을 떨어뜨렸다고 생각하자
그러면 한 방울의 코피나 잉크가 퍼지는 것을 우리는 본 적 있을 것이다. 이런 현상이 확산이다.
정리하자면 확산은 고농도 영역(코피나 잉크 한방울이 떨어지는 지점)에서 저농도 영역(코피나 잉크 한방울이 퍼지지 못한곳)으로 이동하는 메커니즘을 확산이라한다.
반도체에서도 동일한 메커니즘으로 동작하는데 전하 캐리어가 반도체에 주입(떨어짐)되면 불균일 농도(고농도와 저농도 영역이 생김)를 형성한다.
따라서 전기장(E)가 인가되지 않아도 캐리어는 낮은 농도의 영역으로 이동하여, 불균일성이 유지되는 한 전류를 생성한다.
계산과정을 생략하고 전류에 대해 적으면 아래와 같다.
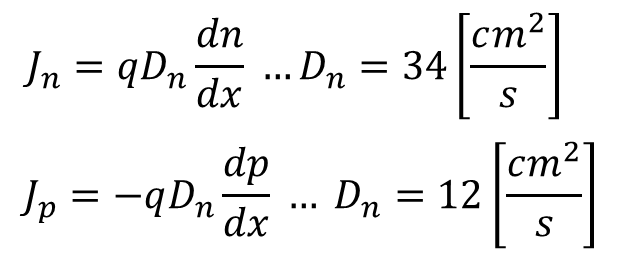
식 7, 8에서 n은 전자, p는 정공을 의미하며, dn/dx 또는 dp/dx는 전류가 x축으로만 흐를 때 x 축에 대한 농도 기울기(slope)이다. Dn 또는 Dp는 확산 계수(Diffusion Coefficient)이다. 위 식에 대한 설명을 토대로한 그림은 아래와 같이 표현 가능하다.
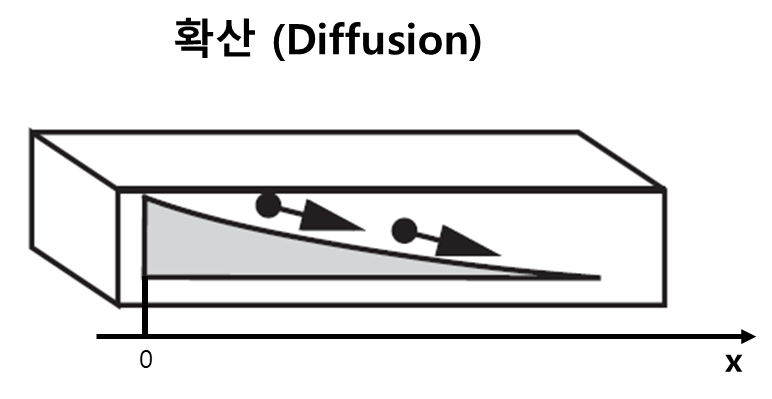
전체 전류 밀도는 아래와 같다.
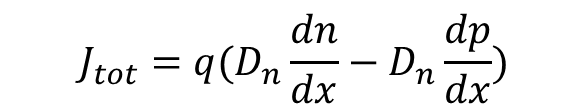
드리프트와 확산을 좀 더 정리해보면
전류를 만드는 두 가지 메커니즘은 확산과 드리프트에 의한 전류임을 알았다.
드리프트는 전기장(E)에 의해서 발생하는 전류고 확산은 전기장(E)가 인가되지 않았도 농도가 불균일 할 때 생기는 전류임을 다시 상기하자
이는 뒤에서 다룰 PN 접합, BJT, MOSFET를 다루는데에 있어 매우 중요한 내용이다.
아인슈타인 관계(기억하면 좋은 내용)
이동도와 확산계수에 대한 관계는 아래와 같이 정의 된다.
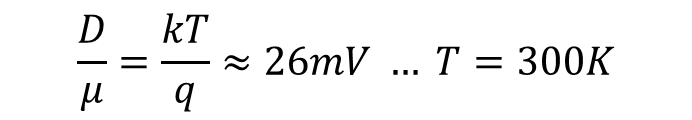
아인슈타인 관계에서는 확산 계수와 이동도의 비는 kT/q를 가지는데 이는 매우 유용하다. Room Temperature(T=300K) 일 때 26 mV를 가진다.
전자회로 1 과정을 학습하셨습니다.
아래 링크를 통해 다음 진도와 전자회로 1의 모든 내용을 확인하실 수 있습니다.

2022.01.13 - [전공(Major)/전자회로 1 과정] - 전자회로 1 커리큘럼
전자회로 1 커리큘럼
전자회로 1 커리큘럼입니다. 기본적으로 반도체 공학에서 배웠던 능동소자(Diode, BJT, MOSFET)를 통해 단일 증폭기를 설계한다. 회로를 해석하는데에 있어 회로이론에서 배운 회로 해석기법을 사용
doctorinformationgs.tistory.com
'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 다이오드의 대신호(Large-Signal)와 소신호(Small-Signal) 동작에 대해 알아보자 (0) | 2022.02.17 |
|---|---|
| 바이어스(Bias)의 의미와 PN 접합의 평형 상태, 순방향 바이어스, 역방향 바이어스에 대해 알아보자 (0) | 2022.02.11 |
| 피드백 회로의 주파수 보상과 밀러 보상(Frequency Compensation and Miller Compensation of Feedback Circuit) (1) | 2022.01.27 |
| 피드백 회로의 위상 마진(Phase Margin) (0) | 2022.01.26 |
| 진성(고유,intrinsic) 반도체와 외부(외인성, extrinsic) 반도체에 대해 알아보자 (0) | 2022.01.25 |




댓글