참조 문헌
1. Probability and Statistics for Engineers and Scientists , Walpole, Myers, Myers and Ye
2. Statistics for Management and Economics, Keller
이 포스팅은 기존의 확률 실험과 이어진 내용입니다. 이전 포스팅에서 제시된 예제가 이어지니 참고하시기 바랍니다.
2021.09.11 - [고등 수학/확률과 통계] - 확률 실험 - 2주차 정리
확률 실험 - 2주차 정리
참조 문헌 1. Probability and Statistics for Engineers and Scientists , Walpole, Myers, Myers and Ye 2. Statistics for Management and Economics, Keller 확률 실험(Random Experiment) 실험의 결과를 예측..
doctorinformationgs.tistory.com
확률의 정의에는
1. 고전적 확률
2. 경험적 확률
이 두가지가 있다 일반적으로 고전적 확률을 많이 쓴다.
사건의 확률을 구하기 위해 파악해야 할 것
1. 표본공간에는 원소가 몇 개 있는가
2. 우리가 관심이 있는 사상에는 원소가 몇 개 있는가
고전적 확률의 정의
사상(또는 사건 event)가 발생할 확률은 사건 A의 원소 개수를 표본공간의 원소로 나뉘어진 값이다.

사건 A가 발생했다하면 확률 실험의 결과가 A의 원소이면 사건 A가 발생했다고 한다.
경험적 확률의 정의
n 번의 확률실험을 했을 때 사건(or 사상) A 가 발생하는 확률 즉 실행 횟수분의 그 사건이 발생한 횟수를 나타낸다.

식 2에서 n(A)는 사건 A의 발생 횟수이다.
그래서 경험적 확률은 실제로 일어나는 결과들을 무한 반복했을 때의 횟수를 비율로 정의.
이해를 돕기 위한 예제 1.
두 개의 주사위를 동시에 굴렸을 때 , 나타나는 숫자의 합이 9가 될 확률은 얼마인가(주사위 수의 범위는 1-6까지)
주사위 2개의 표본 공간은
S={(1, 1), (1, 2) ... (6, 6,)} ... 36개의 원소
9가 될 확률은
(3, 6) (4, 5,) (5, 4) (6, 3)
따라서 P(합이 9) = n(A)/n(S)=4/36=1/9
순열(Permutation)
n 개의 원소 중에서 우리가 r 개의 원소를 선택해서 순서를 고려 하여 나열하는 경우에 출현 가능한 결과의 수를 찾아낼 때 사용하는 방법

순열에서는 순서를 고려하는 점이 중요하니 계산을 할 때 유의하도록 한다.
조합(Combination)
n개의 원소 중에서 우리가 r개의 원소를 선택해서 순서에 관계없이 나열하는 경우에 출현 가능한 결과의 수를 찾아낼 때 사용하는 방법이다.

식 4를 통해 알 수 있는 것은 r!의 영향으로 인해 조합은 순열보다 낮은 값이 나오게 된다.
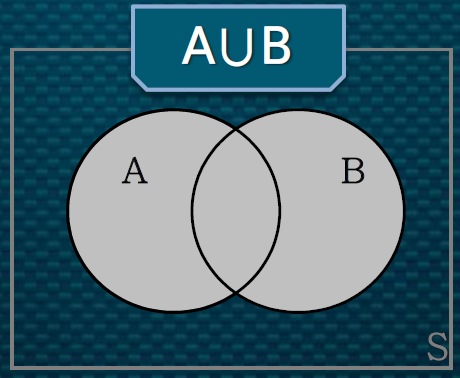
합집합과 교집합의 확률
1. A와 B의 합집합이 발생하는 확률
𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵) / 교집합에 있는 부분은 2번 계산이 되니 교집합 부분을 없애줘야한다.
2. 만약 A 와 B 가 상호배반이라면 확률은 0이다. / 원소가 없기 때문에
𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)

확률의 공리(axioms of probability)
확률의 공리는 표본공간(S)이 정의되고 , 임의의 사건 A 가 있을 때를 말한다.
1. 𝟎≤𝑷(𝑨)≤𝟏
사건 A 가 발생할 확률은 반드시 0 과 1 사이이며 가장 작은 사상은 공집합이다. 마지막으로 가장 큰 사상은 표본공간 ‣ 사상 A 는 공집합과 표본공간의 그 중간에 있기 때문이다.
2. 𝑷(𝑺)=𝟏
표본공간이 발생할 확률은 1 이라는 의미 = 표본공간은 항상 발생하며 확률실험을 하면 결과가 발생하고 그 결과는 표본공간의 원소이기 때문이다. P(S)=1 인 경우 공집합이 발생할 확률은 0.
3. 만약 사상 𝐴1, 𝐴2등이 서로 상호배타면(𝑃(𝐴1∪𝐴2∪⋅⋅⋅)=𝑃(𝐴1)+𝑃(𝐴2)+⋅⋅⋅)
사상들이 상호배반이면 교집합은 0, 합집합에 대한 확률은 각 사상의 확률의 합
'고등 수학 > 확률과 통계 개인학습 노트' 카테고리의 다른 글
| 확률 변수, 이산형 확률 변수, 연속형 확률 변수 - 3주차 정리 (0) | 2021.09.22 |
|---|---|
| 조건부 확률과 베이즈 정리 - 2주차 정리 (0) | 2021.09.14 |
| 확률 실험 - 2주차 정리 (0) | 2021.09.11 |
| 기초 통계량 - 1주차 정리 (0) | 2021.09.07 |
| 표본과 표본 추출법 - 1주차 정리 (0) | 2021.09.06 |




댓글