참조 문헌
1. Probability and Statistics for Engineers and Scientists , Walpole, Myers, Myers and Ye
2. Statistics for Management and Economics, Keller
확률변수(random variable)
확률 실험의 발생 가능한 결과에 하나의 값을 배정하는 함수이다.
- 주로 확률변수는 영어 대문자 X,Y,Z 등을 사용함
- 모든 확률변수는 고유한 확률분포를 따름
이해를 돕기 위한 예시
동전 1개를 3회 던지는 실험
동전의 앞면을 H, 뒷면을 T라고 가정했을 때
{HHH}{HHT}{HTH}{THH}{HTT}{THT}{TTH}{TTT} 이렇게 8개가 나온다.
확률 변수의 경우는 각각의 결과들을 숫자로 변환을 시켜야 한다.
만약 문제에서 확률변수 "X" = 각 실험의 결과가 갖는 T의 수라고 하였을 때
{HHT}{HTH}{THH} 는 1 / X=1
{HTT}{THT}{TTH} 는 2 / X=2
{TTT} 는 3 / X=3
{HHH}는 0 / X=0 이 나오게 된다.
이산형, 연속형 확률변수를 알아가기 위해서는 집합의 종류에 대해 알아야 합니다.
집합의 종류
유한 집합 : 원소의 수가 유한한 경우 (예 {0, 1, 2, 3})
셀 수 있는 무한집합 : 원소의 수가 무한 개이지만 셀 수 있는 경우 (예 : 1, 2, 3 ...)
셀 수 없는 무한집합 : 원소의 수가 무한이며 셀 수 없는 경우 ( 155.5 <X<180.2 .. 소수점까지 생각하면 셀 수 없음)
이산형 확률변수(discrete random variable)
확률변수 X 의 Rx 가 유한 집합 또는 셀 수 있는 무한집합의 경우, 확률변수 X는 이산형 확률변수라고 함
확률함수 (probability function)
f(x)는 probability 확률변수 X가 스몰 x를 갖는 확률이 된다.(X는 확률 변수, x는 확률 변수 X가 갖는 값 중의 하나
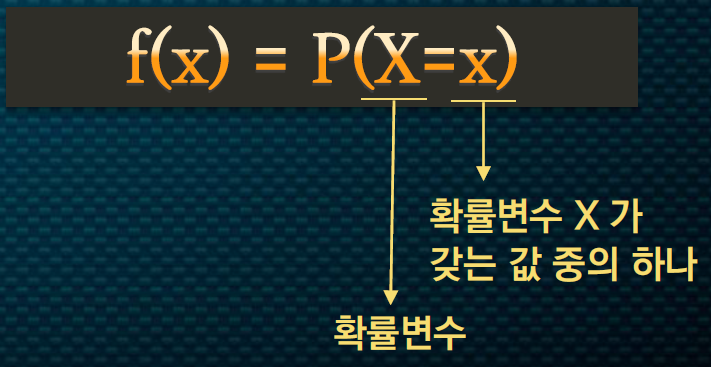

모든 값에 대한 f(x)의 합은 1이고 확률의 공리로 인해서 0~1의 범위를 갖는다.
연속형 확률변수(continuous r.v.)
확률변수 X 의 RX 가 셀 수 없는 무한집합의 경우, 확률변수 X는 연속형 확률변수라고 함
밀도함수(density function)
f(x) 는 확률변수 X 가 값 x에 대해 밀집된 정도를 나타내는 함수
밀도함수의 특징은 아래와 같으며, 여기서 X 는 연속형 확률변수 , a 와 b 는 상수이다
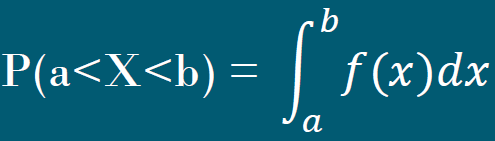

밀도함수는 무조건 양의 함수여야 하고 마이너스 무한대에서 플러스 무한대까지 밀도함수를 적분했을 때 총 면적은 1이다.
연속형 확률변수 X는 어떤 특정한 값을 가질 확률은 𝑃(𝑋=𝑥)=0 이므로, 𝑃(𝑎<𝑋<𝑏)=𝑃(𝑎≤𝑋<𝑏)=𝑃(𝑎<𝑋≤𝑏)=𝑃(𝑎≤𝑋≤𝑏) 이 네가지 확률이 동일하며 부등호에 민감하지 않다.
(여기서 X 는 연속형 확률변수 , x 는 X 가 갖는 값 중의 하나이다 .)
문제 1. 다음 함수가 확률함수인지 확인하라
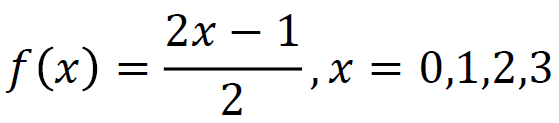
풀이
x가 0일때 -0.5 이므로 확률 변수의 범위 밖에 있어 확률 함수가 아니다. 따라서 나머지를 확인 할 필요가 없다

풀이 : 모든𝑥에대하여𝑓(𝑥)≥0 이고 모든 𝑓(𝑥)의 합이 1이므로 확률함수이다.
문제 2. 𝑓(𝑥) 가 밀도함수가 되기 위한 k 의 값을 구하라
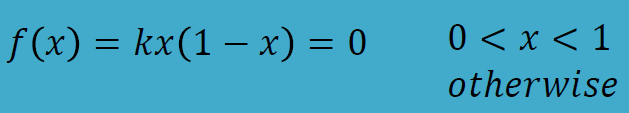
풀이
풀이를 하기에 앞서 밀도함수의 특징을 통해 주어진 문제가 밀도함수인지 확인하기 위해서 위에서 언급한 두 조건을 확인해 본다.
1) f(x)<= 0 이 조건을 만족한다.
2) 모든 구간에서 1이 되는지 확인을 해야한다.
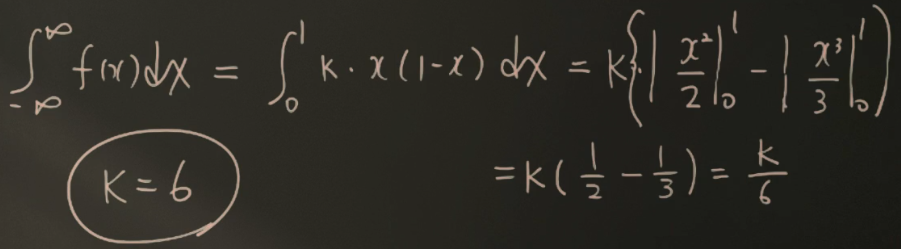
따라서 K=6이여야 한다.
문제 3. 확률변수 X 는 아래의 밀도함수를 가지며 네모 칸 안에 표기된 다음의 확률을 구하라.
(1) Ρ(−1<Χ<1/2) = 1/8 ... 정답
(2) Ρ(Χ≤3/2) = 7/8 ... x의 구간을 확인하면 2 구간이 나와 적분하면된다.
(3) Ρ(Χ≥2.5) = 0 ... x의 구간이 2보다 크면 0
(4) Ρ(3/4<Χ<3/2) = 27/32 ... 이것도 동일하게 2 구간이 나옴으로 두 구간에 대해 적분의 범위를 적어주고, 계산하면 된다

이전 진도
2021.09.14 - [고등 수학/확률과 통계] - 조건부 확률과 베이즈 정리 - 2주차 정리
조건부 확률과 베이즈 정리 - 2주차 정리
이전 진도 2021.09.11 - [고등 수학/확률과 통계] - 확률의 정의 - 2주차 정리 확률의 정의 - 2주차 정리 참조 문헌 1. Probability and Statistics for Engineers and Scientists , Walpole, Myers, Myers and Ye..
doctorinformationgs.tistory.com
감사의 글
소정의 지식을 쌓는데에 도움이 되셨다면 광고 클릭을 하여 불쌍한 대학원 노예에게 10원의 기부를 부탁드립니다.
'고등 수학 > 확률과 통계 개인학습 노트' 카테고리의 다른 글
| 이변량 확률변수, 결합확률함수, 결합밀도함수, 주변확률함수, 공분산 - 4주차 정리 (0) | 2021.09.27 |
|---|---|
| 분포함수, 확류 변수의 평균과 분산, 함수 - 3주차 정리 (0) | 2021.09.22 |
| 조건부 확률과 베이즈 정리 - 2주차 정리 (0) | 2021.09.14 |
| 확률의 정의 - 2주차 정리 (0) | 2021.09.11 |
| 확률 실험 - 2주차 정리 (0) | 2021.09.11 |




댓글