여러 자료들을 종합하다보니.. 내용이 산으로 가는 느낌이 든다.
혼란 스러워도 넓은 이해심을 가져주시면 감사하겠습니다.
단방향과 양방향 피드백
한방향 피드백(Unilateral Feedback)

한방향 피드백은 신호가 한방향으로만 이동하는 것을 의미한다.
이는 전자회로 2에서는 그림 1과 같은 내용의 회로를 배웠을 것이며 이번 글은 상급 교재의 내용으로 양방향 피드백을 알아가고자 할 것이다.
양방향 피드백(Bilateral Feedback)

양방향 피드백은 신호가 두개의 방향으로 이동함을 의미하고 있습니다.
이제 그림 1과 2에 있는 A_∞, d, T, 반환율에 대해 알아보자
반환율(Return-ratio) 해석 : 반환율 해석은 최소한의 근사치로 정확한 결과를 산출한다.
A∞ : 피드백 회로가 이상적일 때 폐쇄 루프 이득(Closed-Loop Gain)이다. main 증폭기의 이득을 무한대로 설정하고 Sout/Sin을 찾아 얻을 수 있다.
d : 피드-포워드 항이며 main 트랜지스터 증폭기의 gm을 0으로 설정하고 Sout/Sin을 찾아 얻을 수있다.
T : 루프 이득(Loop gain)이며 입력 해제 한 다음에 gm과 병렬로 테스트 전류원을 추가하고 gm의 출력 경로를 끊고 접지로 전환을 한 다음에 -1* 복귀 전류의 값을 구하여 구한다.
입/출력 관계
입출력 관계에 대한 식은 아래와 같이 주어진다.

식 1을 통해 알 수 있는 점은 만약 T가 증가하면 피드백은 전달함수의 T에 대한 의존성을 감소시키고 피드포워드 경로를 억제(Suppress)함을 알 수 있다.
좋은 피드백에 대한 요구사항들은 아래와 같다.
1) 높은 루프 이득(또는 반환율)2) 낮은 피드-포워드 이득3) 포워드 이득(A∞T)은 피드백 계수(1/A∞)의 영향을 크게 받지 않아야 합니다.
• 영향을 크게 받게 된다면 피드백 효과는 피드백 계수(일반적으로 설계 파라미터)의 영향을 받는데, 이는 바람직 하지 못한다.
피드백 회로의 보데 해석을 이해하기 위한 계수 해석
(Coefficient interpretation to understand the Bode`s Analysis of Feedback Circuits)
아래에서 해석이란 단어는 "Interpretation" 이란 단어로 쓰였다. 영-영 사전을 통해 알아보게 되면 아래와 같다.
Interpretation : the act or result of explaining or interpreting something; the way something is explaimed or understood
아래의 계수를 구하기 위해 어떤 과정으로 답을 얻는지에 대해 알아보도록 한다.
이전에 단원(Chapter)들에서 회로 해석을 할 때 출력 전압으로 소신호 이득(Small-Signal Gain) 또는 전달 함수(Transfer Function)를 구할 수 있음을 알 수 있었다.

종속 전류원(또는 종속 전압원)을 전류 "I1" 으로 표기하고 이는 독립 전류원이라고 생각해야 한다. 출력 전압에 대한 식으로 정리하면 입력 전압과 전류 "I1"으로 표현이 가능하며 이는 아래와 같이 표현이 가능하다.
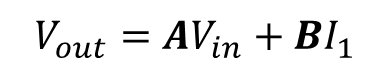
식 2에서 첫번째 항의 A는 입력 전압으로 부터 피드쓰루(Feedthrough)된 양을 의미하고 B는 종속 전원으로 부터 곱해지는 저항성분을 가짐을 알 수 있다.
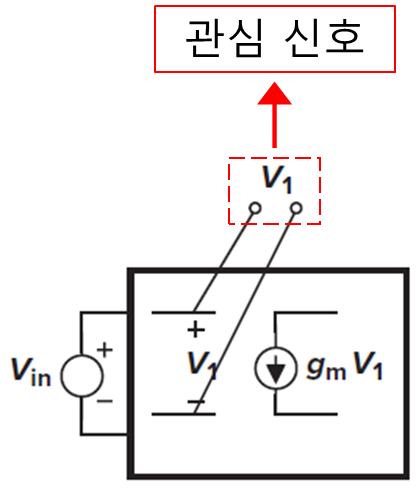
그림 3과 동일한 방법으로 종속 전류원은 "I1" 즉 독립 전원으로 표현하며 관심 신호는 V1이다. 여기서 V1을 "출력"으로 간주하여 계산하면 아래와 같다.
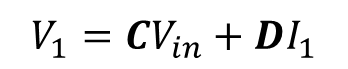
식 3에서 계수 C는 입력 전압으로 분배된 양을 의미하는 것 같고, D는 뒤에서 언급하게 될 루프 이득과 관련이 있다.
(이 부분은 제 개인적인 해석이니 틀릴 수 있습니다. 틀렸다면 지적 부탁드립니다.)
식 2와 3으로 부터 A부터 D까지의 계수(Coefficient)가 있음을 알 수 있다.
계수 "A" 해석
종속 전류원을 0으로 만들어 gm을 0으로 보내 동작을 못하게(disabling) 하는것, 트랜지스터의 출력 전압(Vout)은 트랜지스터 없이 입력신호의 피드쓰루(feedthrough)로 생각한다.
정리하자면 트랜지스터가 동작을 하지 않아도 그림 2와 같이 입력신호가 출력 신호에 바로 가는 것을 의미한다.
이는 피드백 계수 해석중 "A"에 해당하며 피드백 계수 A는 Vout/Vin 이고, 종속 전류원이 0인 경우에 대해 얻어지는 값이다.
계산 과정은 아래 그림으로 얻어진다.
계수 A는 아래와 같이 얻어진다.
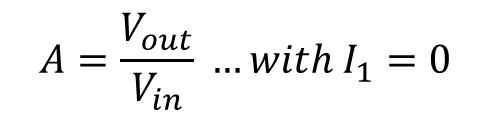
그림 5에서 입력 전압이 출력 전압으로 갈 수 있는 경로(Path)가 있다면 A=0이 아니게 된다.
내용의 흐름을 위해 B는 뒤에서 설명하고, 계수 C를 보도록 하자
계수 "C" 해석
계수 C도 A와 비슷한 방법으로 계산된다. gm=0으로 두어 입력에서 V1(Vgs) 까지의 전달 함수를 구하는 것이다.
A와 동일한 gm=0이기 때문에 트랜지스터는 동작하지 않는다. 따라서 아래와 같이 구해짐을 알 수 있다.
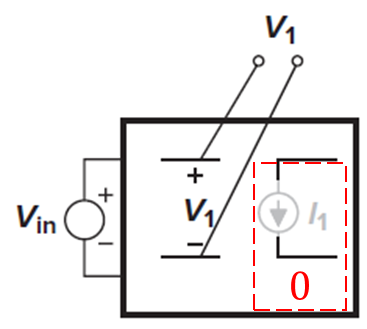
계수 C 역시 트랜지스터가 동작하지 않기 때문에 축퇴 저항과 같은 수동 소자가 존재해도 전류가 흐르지 않는다는 것을 유의하기 바란다.
계수 C는 아래와 같다.
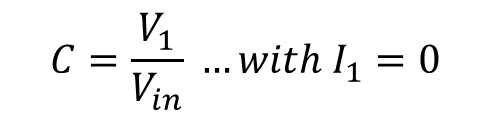
계수 A, C의 공통점은 트랜지스터가 동작하지 않는다는 것 즉 I1=0 이라는 점을 인지하길 바란다.
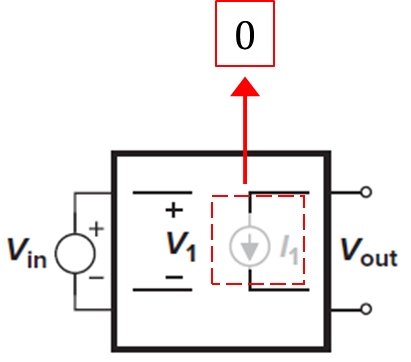
계수 "B" 해석
계수 B는 입력을 0 으로 만들고 종속 전류원(I1)이 외부 입력에 영향을 받지 못하게 독립 전원인 것 처럼 생각해 I1의 결과로 출력 전압(Vout)을 계산한다.
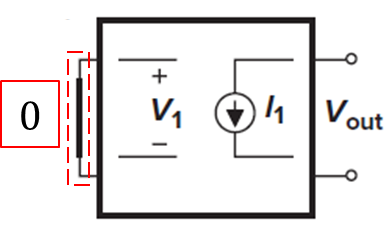
그림 7에서 독립 전원(I1)의 결과로 출력 전압을 계산할 수 있다. 따라서 아래와 같이 계산 방법을 가질 수 있다.
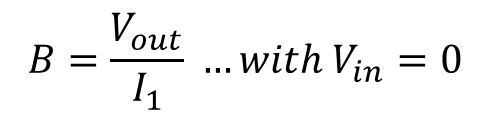
계수 "D" 해석
계수 D는 B와 동일하게 입력을 0으로 하고, I1에서 V1까지의 전달 함수를 나타낸다. 이는 B와 비슷한 방법이며 무엇을 얻는지에 대한 차이점을 명확하게 이해하면 좋을 듯 싶다.
계산 방법은 아래와 같이 구할 수 있다.
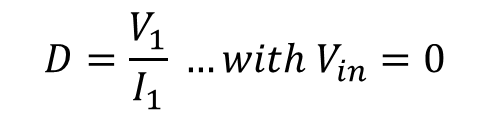
이를 정리하면 아래와 같은 표로 표현할 수 있다.
| 계수 | 무엇을 바꾸는가? | 무엇을 구하는가? |
| A | gm=0 | 출력 전압 |
| B | 입력 전압(또는 입력 전류)를 0 | 출력 전압 |
| C | gm=0 | V1 |
| D | 입력 전압(또는 입력 전류)를 0 | V1 |
이를 상기함으로써 보데 해석으로 넘어갈 수 있다.
보데 해석(Bode`s Analysis)
위에서 얻어진 식을 Vout과 V1에 대해 정리하면 아래와 같다.

V1에 대한 식에서 I1을 gmV1으로 치환하고 계산하게 되면 아래와 같은 식을 얻는다.
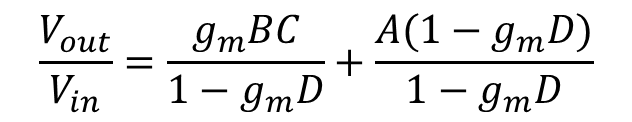
식을 정리하면 아래와 같다.
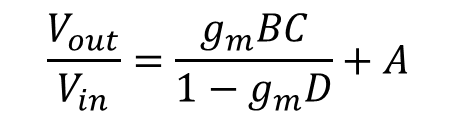
식 10 어디선가 많이 본 식 같은데 이는 식 1과 비슷한 형식으로 얻어지는 것 같다.
계수 A는 피드쓰루이며 (1-gmD)는 루프 이득이면서 반환율(Return Ratio, T, RR)이다.
위 과정들은 전압-전압에 관한 내용이다. 따라서 다른 방법에 대해서는 해당 계수를 따로 구해야 한다는 것을 참고해야 한다.
식 1과 그림 2를 유도하는 과정에 대해 조금 더 다뤄보도록 한다.
반환비(또는 반환율, Return Ratio, T, RR)
반환비(T, RR)를 계산하기 위한 절차
1) 모든 종속 전원을 0으로 설정
2) 반환비를 찾기 위한 종속 전원을 선택한다.
3) 종속 전원이 전류(또는 전압)의 전원의 형태라면 같은 형태와 극성이 동일한 독립전원을 배치하고 선택된 종속 전원과 함께 병렬로 배치한다.
4) 종속 전원을 삽입된(Inserted) 전원의 옆으로 이동시키고 종속 전원을 독립 전원에 연결하는 두 개의 리드선을 자른다.
5) 전압 전원에서 반환비는 절차 3번에서 언급된 독립 교체 전원의 전압과 종속 전원에 걸쳐진 전압을 나누어진 (-)의 비이다.
6) 전류 전원에서 종속 전원의 끊어진 리드선을 단락한다. 반환 비는 독립 교체 전원의 전류와 단락 회로 전류의 결과의 (-) 비이다.




댓글