이 글은 Feedback Chapter의 첫 글이며 형식상 귀환 또는 궤환이라는 단어보다 피드백이라는 단어가 더 편하니 앞으로의 글은 피드백으로 부르도록 하겠다.
그리고 해당 포스팅은 단방향(Unilateral) 피드백이라고 가정하여 글을 쓰게 되었다.
양방향 피드백인 경우는 모든 진도를 끝내고 적어보도록 하겠다.(이 내용은 상급 교재에 수록이 되어있음)
피드백... 너란 녀석을 알아보자
간략하게 서론을 떠들어본다면.. 피드백은 앞 부분을 잘 다루어야한다. 왜냐하면 다른 chapter 내용들과 다르게 앞 내용이 완벽하게 이해가 가지 못한 상태로 뒷 부분을 읽게 될 때 무슨말이지? 할 수 있기 때문이다.
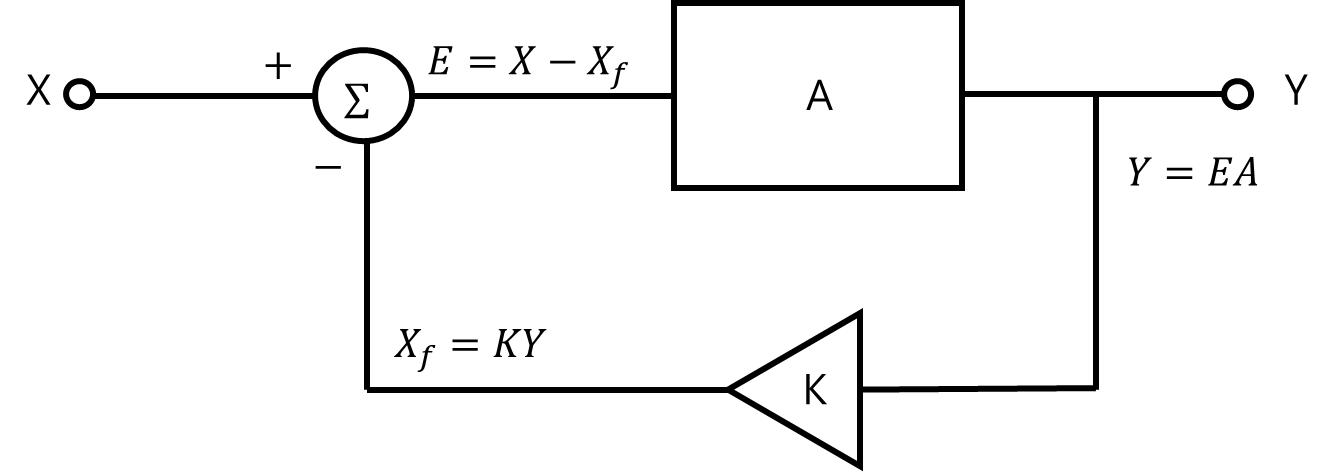
아래의 그림 1과 같이 일반적인 피드백 시스템을 보자

여기서 X는 입력신호, 증폭기가 가지는 이득인 A, Y는 증폭되서 나온 출력 신호, K는 귀환율(Feedback Factor)이다.
그림 1에서 유심히 보아야 하는 것은 입력신호와 출력신호가 귀환율을 지나 어떤 출력(Xf)를 만들고 이 신호가 입력신호 X와 빼지는 관계를 형성한다.
여기서 어떤 출력(Xf)은 귀환 신호이며 입력신호와 귀환신호의 차이는 오차(E)라고 표현된다.
이를 수식과 함께 정리하자면 아래 같이 정리가 가능하다.
Step 1)
어떤 입력 X가 A배의 증폭기를 통해 신호가 증폭이 되어 출력(Y)에 나온다.

Step 2)
출력 Y는 피드백 네트워크에 입력으로 가게되며, 이는 귀환율과 출력의 곱의 형태인 피드백 신호를 만든다.

Step 3)
이 피드백 신호는 음의 신호를 가지게 되며 양의 입력신호(X)와 합쳐져 오차(E)를 만들어 낸다.

Step 4)
이 오차는 다시 어떤 증폭기의 입력신호가 되며 증폭기의 출력 Y는 다음과 같이 표현 가능하다.
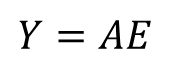
식 4에서 식 3을 넣고 식 3에 식 2를 대입하면 아래와 같이 입출력 관계식을 얻을 수 있다.

식 5와 같은 형식을 폐루프 이득(Closed-Loop Gain)이라 부르며 아주 중요한 식이다.
만약 귀환율 K가 없다면 입출력 방정식은 어떤 이득 "A"만 나오며 이는 개루프 이득(Open-Loop Gain)을 의미한다.
뒤에서 언급하겠지만 피드백 네트워크를 통한 이득 즉 폐루프 이득은 개루프 이득보다 낮음을 알 수 있는데 나쁜건 아니라고 말하고 싶다. 이득을 헌납하고 이득 둔감화, 선형성 향상, 대역폭 확장, 입출력 임피던스의 변화라는 특징을 가져오기 때문이다.
식 5에서 얻어지는 KA는 귀환율과 증폭기 이득 A의 곱으로 표현이 되어 있음을 다시 생각해볼 수 있다.
피드백 루프(Loop)를 통해 얻어짐을 알 수 있으며 KA는 루프 이득(Loop Gain)이라 부른다.
루프 이득에 대해서는 다음 소주제에서 좀 더 살펴 보도록하고 기본적인 부분들을 더 다뤄보겟다.
식 5에서 입력신호(X)가 어떤 증폭기가 A의 이득을 만드는 회로에 입력이 들어와 Y로 출력이 되고, Y는 다시 피드백 네트워크로 입력이 되어 피드백 신호 Xf를 만든 다음에 입력신호와 피드백 신호의 차가 다시 A의 이득을 가진 증폭기에 들어와 피드백을 가진 이득을 만든다.
따라서 Y/X=Af라 적을 수 있고 이는 피드백을 가진 이득(gain with feedback)이라 부른다.
식 5는 아래와 같이 정의 될 수 있다.
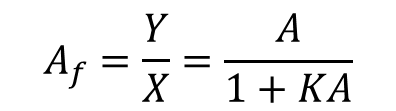
루프이득(KA)가 1보다 한참 크게 되면 식 6은 아래와 같이 간단해질 수 있다.
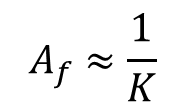
식 7에서 알 수 있는 내용은 루프이득이 클 때, 피드백 증폭기의 이득은 피드백 네트워크에 의해서 결정된다.
(일반적으로 식7과 같은 결과를 Af의 이상적인 값이라고 간주한다.)
귀환 신호인 Xf에 대해 다시 한번 고려보자.
식 3, 식 4, 식 2를 순서로 E에 대해 계산하면 아래와 같다.
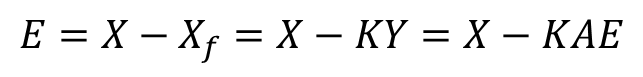
식 8을 정리하면
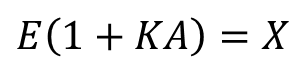
다시 에러에 대한 식으로 정리하면 아래와 같다.
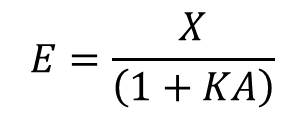
루프이득(KA)이 1보다 한참 클 때 입력 신호 X가 매우 작아지는 것을 증명할 수 있다.
네거티브 피드백(Negative Feedback, 부귀환)이 기본 증폭기의 입력 단자들에 나타나는 신호를 1+KA만큼 감소 시킨다. (1+KA를 귀환양이라고도 부름) 이러한 결과는 입력신호의 감쇄로 인해 이득이 감소함을 알 수 있고 이는 피드백 증폭기의 선형성이 개선(이득이 떨어짐으로 대역폭 또한 증가)되는 것을 알 수 있다.
루프 이득(Loop Gain)
앞서 다룬 내용들에서 KA 즉 루프 이득이 계속 나옴을 알 수 있고, 이는 중요한 파라미터 특성임을 확인할 수있다.
그러면 우리는 루프이득(KA)을 구하기 위해 어떤 절차를 이용해 알 수 있는지 다음과 같은 과정들을 통해 알 수 있다.
절차 1. 입력 신호(X)를 없앤다 즉 X=0으로 만들기 위해 접지 시킨다.
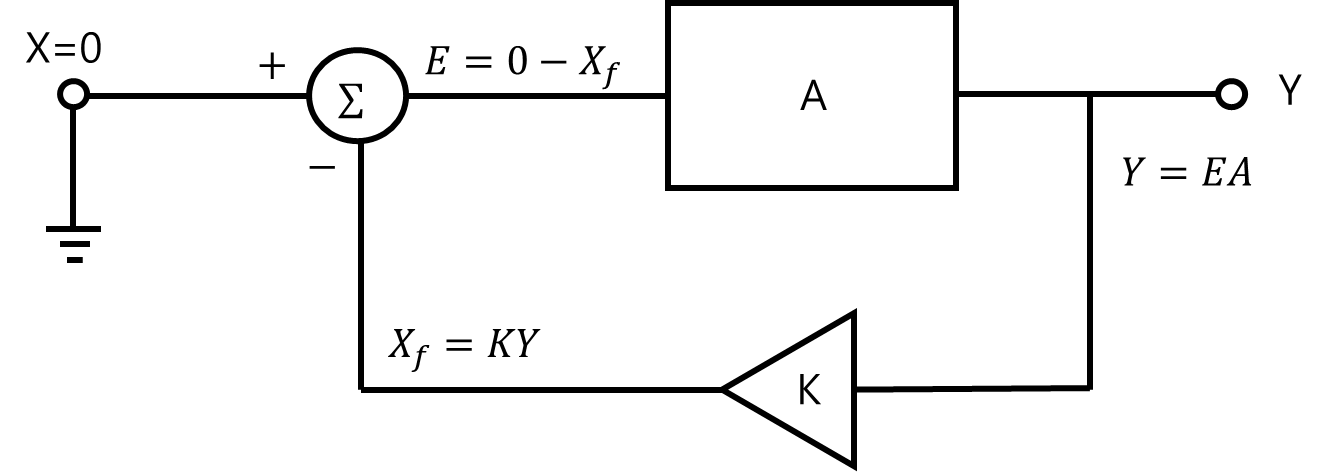
절차 2. (K와 A값이 바뀌지 않는 선에서) 귀환 루프를 끊는다.
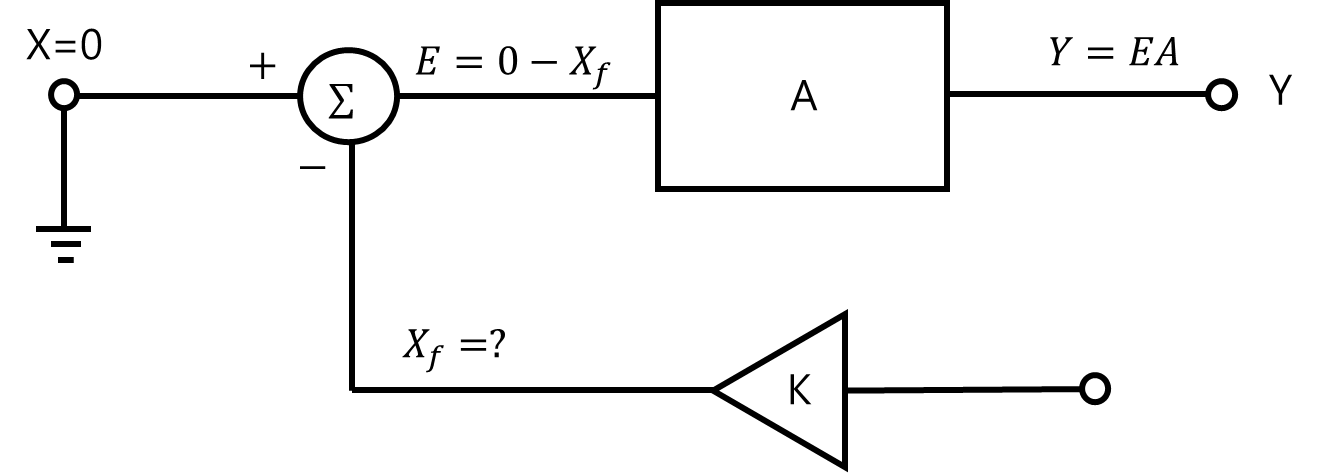
절차 3. 테스트 신호(Vt)를 루프의 입력으로 인가하고,
루프의 출력(Y)에서 돌아오는 신호를 Vn을 구한다.
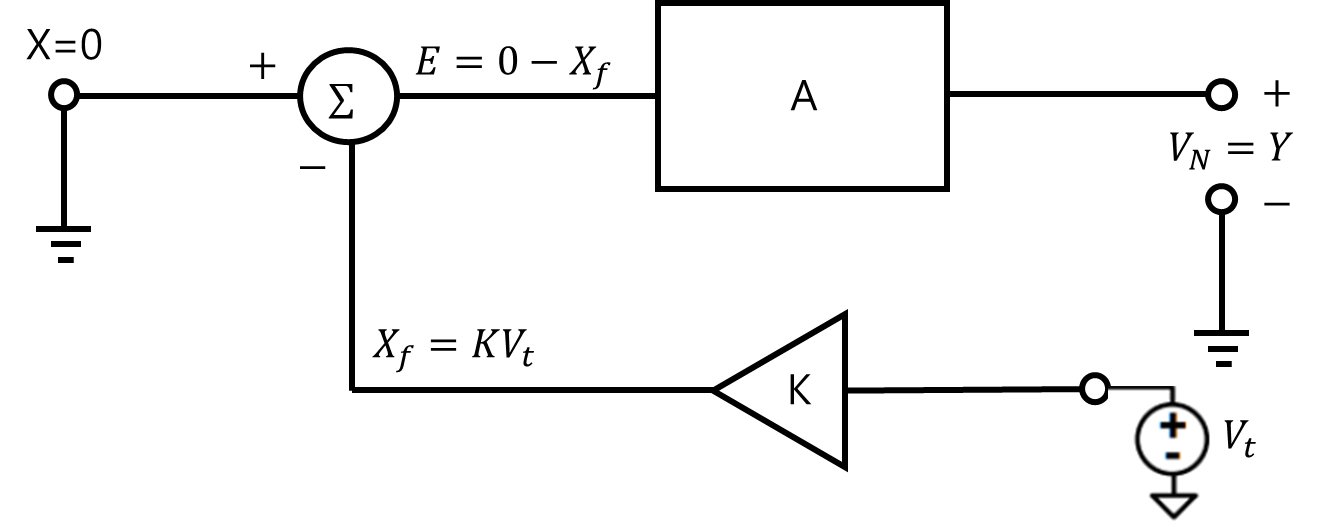
이를 통해 Vn은 아래와 같다.
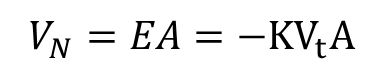
출력/입력에 대한 식으로 쓰게 되면 아래와 같다.

폐루프 이득(식 6, Closed-Loop Gain)과 루프 이득(Loop Gain)을 혼동하지 않도록 한다.
같은 절차로 아래의 그림도 한번 보도록 하자
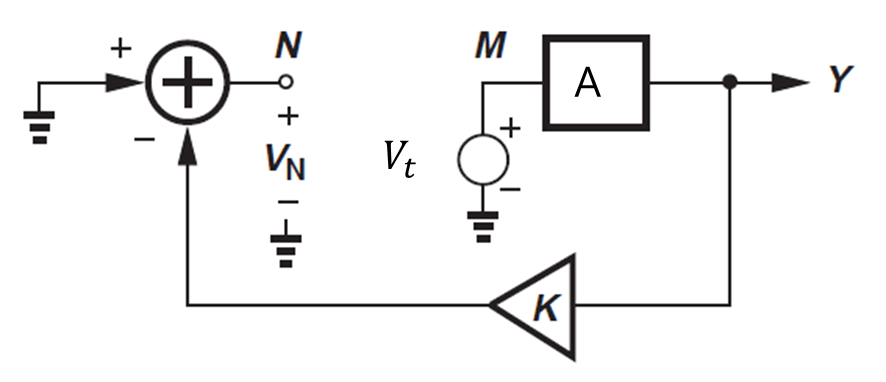
Vt의 테스트 전압이 A배 증폭이 되서 Y=VtA가 되며 이 신호는 피드백 네트워크로 들어가 Xf=KAVt가 된다.
입력(X)는 0이기 때문에 E=0-KAVt 가 되고 Vn=E 임으로 Vn/Vt = -KA 가 된다. 이는 식 12와 동일하게 나옴을 알 수 있고 절차 2에서 K, A가 바뀌지 않는 선에서 귀환 루프를 어디든 끊어도 같은 결과가 나옴을 알 수 있다.

'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 피드백 회로 신호의 감지와 반송 그리고 피드백의 극성 (2) | 2021.12.30 |
|---|---|
| 증폭기의 형태(Types of Amplifier) 또는 증폭기의 종류 (0) | 2021.12.28 |
| 잡음을 고려한 차동증폭기 회로 설계(Design of the differential amplifier considering Noise) (0) | 2021.12.13 |
| 단방향 피드백과 양방향 피드백을 알아보자 (0) | 2021.12.11 |
| 저항과 MOSFET의 잡음해석(Noise Analysis of the Resistor and MOSFET) - 무잡음 신호와 잡음 회로 해석(Noiseless signal + Noise Circuit) (0) | 2021.12.09 |




댓글