개인적인 학습노트입니다.
수업에 쓰였던 자료와 박병하 교수님의 "재능 기부 강의"를 참고했습니다.
바쁘신 와중에 영상을 올려주신 박병하 교수님 감사합니다.
PFD/CP PLL은 아래 그림 1과 같이 전체적이 개략도를 알 수 있다.

PFD 동작의 개념도
Conceptual PFD Operation
PFD는 Phase와 Freq 성분 둘 다 감지하는 장치이다.

A 입력은 Ref 신호를 받고 B 입력은 VCO(또는 Divider를 통해 나온 출력)이고, Q_A는 전하 펌프 드라이브를 UP을 시켜준다.
PFD의 상태도를 먼저 이해하도록 한다.

상태도에서 어떤 신호는 상승 엣지를 감지하며, 상태 0 (State 0)에서 어떤 신호가 들어오느냐에 따라 상태 1, 2, 0을 왔다 갔다 할 것이다.
(1) Ref 와 VCO의 f가 다른 경우

레퍼런스 신호의 주파수가 vco 주파수보다 더 높은 경우 상승엣지가 R에서 먼저 나왔기 때문에 Up 클럭을 생성한다. 일정 시간이 지나고 V도 상승엣지를 가지면 UP, DOWN 둘 다 0인 상태가 된다 이는 그림 3에서 상태 0-1-0에 대해 설명해준 것이다.
그림 4 우측에서는 VCO 주파수가 REF 주파수보다 높으므로 DOWN 클럭이 1이 되고, 잠시후에 R이 상승엣지를 가지면서 상태 0으로 돌아간다 이는 상태 0-2-0 를 예시로 든 것이다.
(2) 주파수는 같지만 위상이 다른 경우
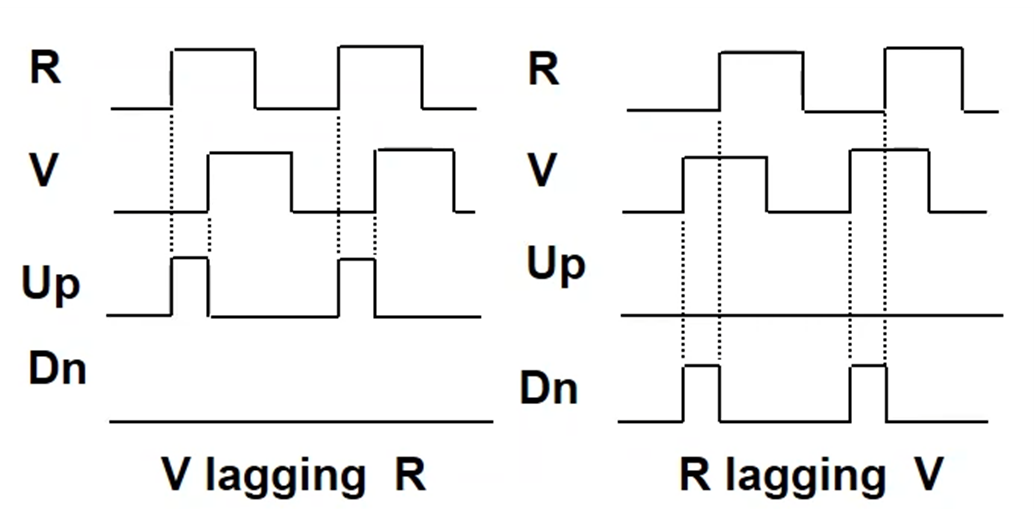
그림 3을 통해 상태 0-1-0, 0-2-0을 반복함을 알 수 있다.
PFD 구현
PDF의 구현은 아래 그림 6과 같다.
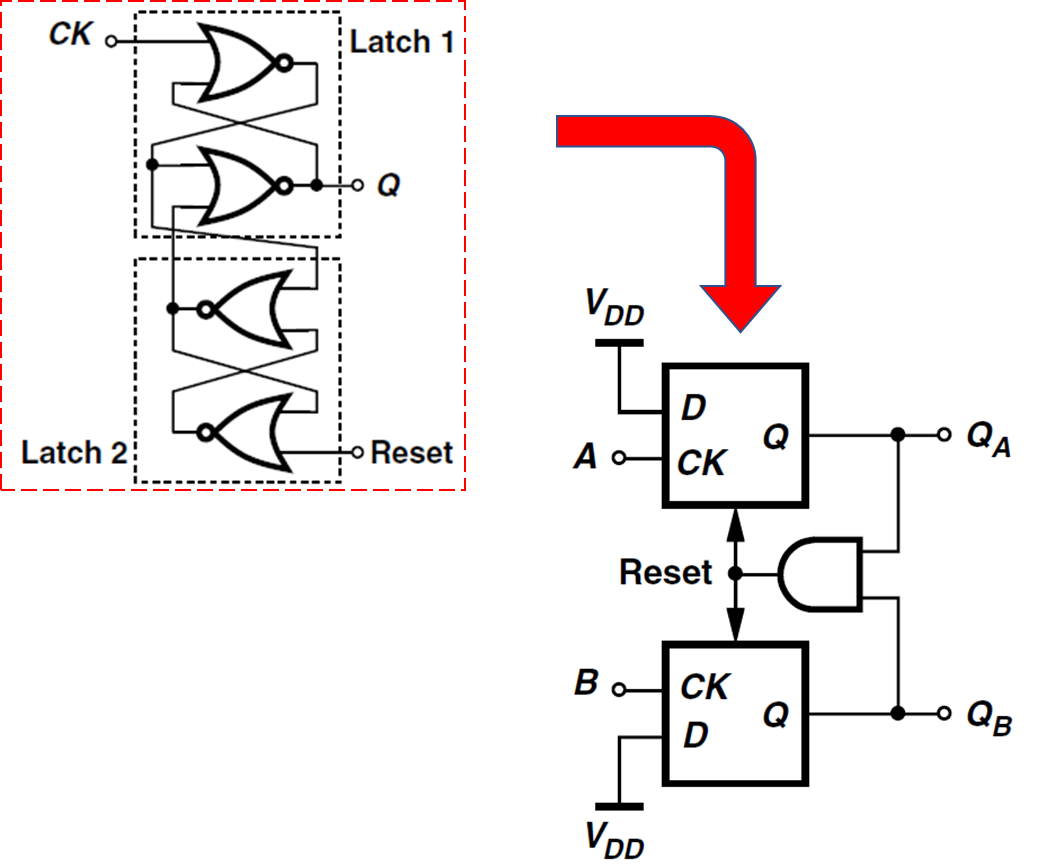
D F/F의 D 단자는 VDD와 연결되어 있고, Clk 단자에는 Ref 또는 VCO 출력이 연결 되어 있음을 알 수 있다. 각각 리셋이 가능한 D F/F은 좌측 붉은 네모 박스로된 로직 게이트로 구현할 수 있다.
전하 펌프
Charge Pump
스위치의 상태에 따라서 C를 충전하거나 방전하는 것을 전하펌프라 한다. C는 DC성분을 만들기 위해(적분) 사용된다.
전하 펌프의 구조
기본적인 전하 펌프는 아래 그림 7과 같다.
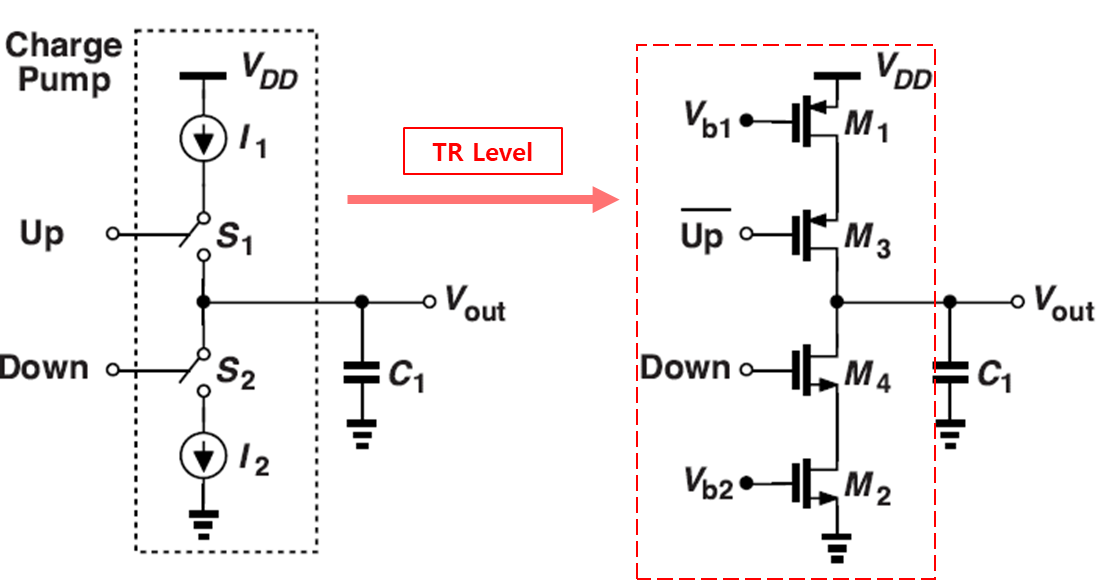
그림 7을 보게되면 UP에는 ` 또는 Bar 가 있다 그 말은 앞에 인버터가 연결됨을 알 수 있다. 이와 같은 구조는 드레인-스위치 CP라고 부른다.
M1, M2는 바이어스 전류를 만들기 위해 있고 전류는 식 1과 같다. 그리고 Up & Down은 QA, QB의 신호를 받게 된다.
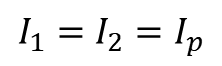
간단한 동작
1) 스위치 둘 다 켜질 때
전하 펌프의 전류는 VDD - gnd까지 흐르기 때문에 C1에 충전이 되지 않는다.
2) M3 가 켜질 때
그림 4, 5 좌측과 같이 REF 신호가 먼저 상승 엣지 일때는 UP(bar)에 신호가 들어오고 M4는 꺼져있다 (Turned-Off) 따라서 전류는 C1에 흐르며 충전이 된다.
3) M4 가 켜질 때
그림 4, 5 우측과 같이 VCO 출력 신호가 먼저 상승 엣지를 경험 할 때 M4가 켜지고 M3가 꺼지기 때문에 충전된 C1의 전류 방전의 경로를 M4를 통해 방전되게 됨으로써 C1에 충전된 전압은 감소하게 될 것이다.
PFD/CP/C 직렬연결에 대해
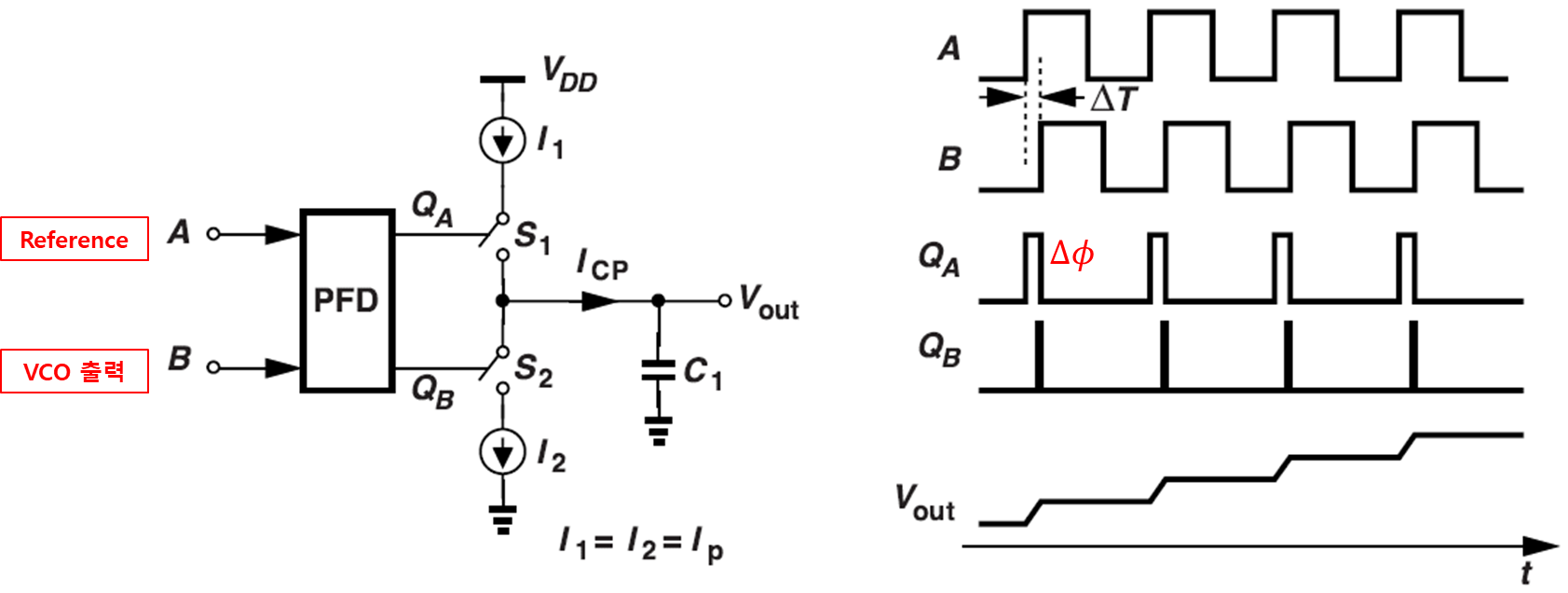
위 내용들에서 Qa 신호가 들어오게 되면 M1이 C를 충전하게 된다. 아래 그림 8을 보도록 하자
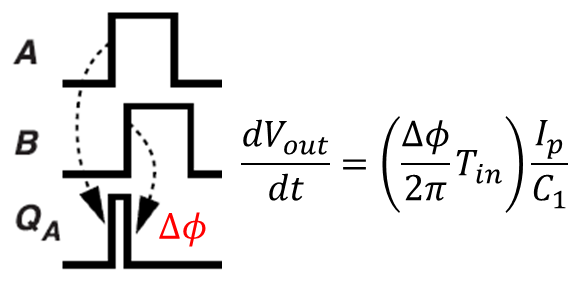
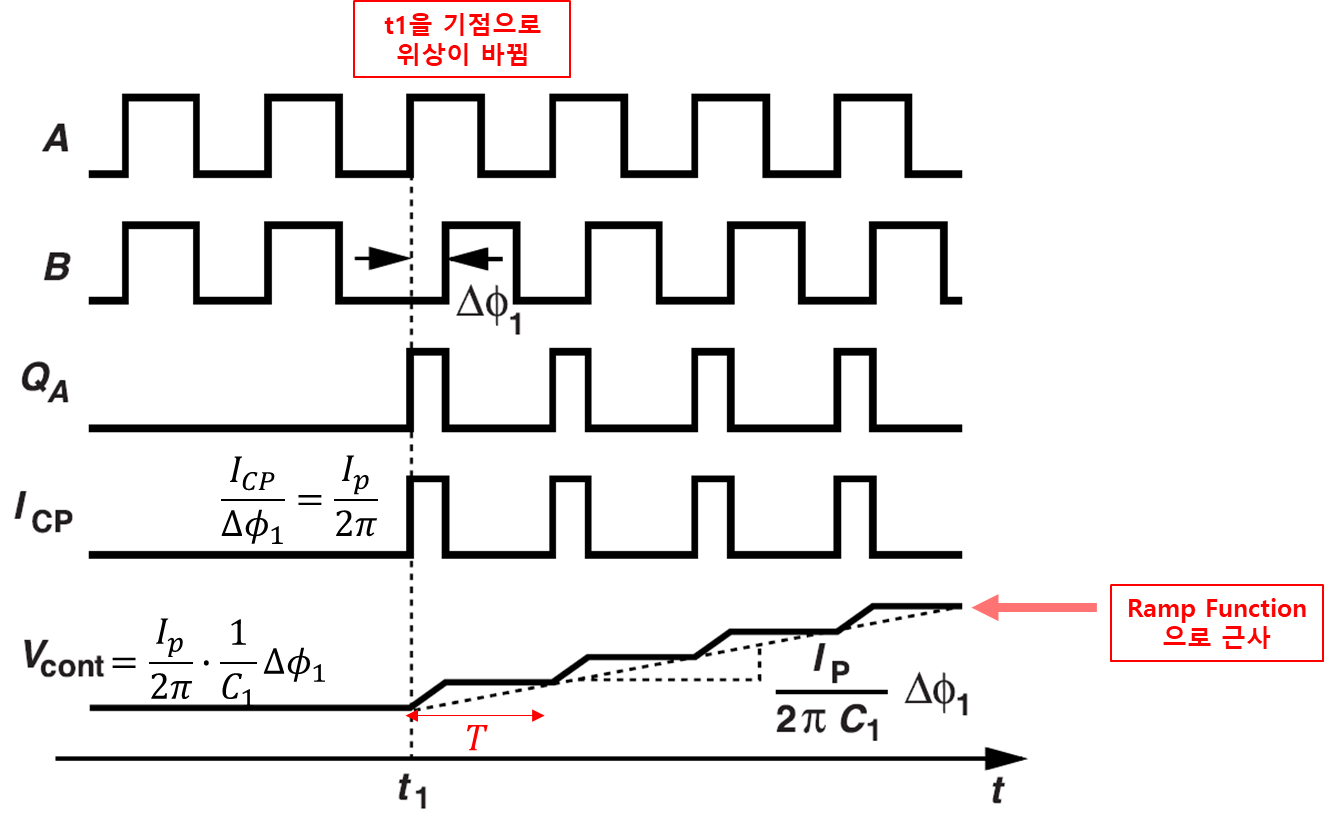
A는 REF, B는 VCO 출력이다. ΔΦ 만큼 Qa는 켜지게 되고 M3가 켜져 C를 충전하게 된다. 시간에 따라 변화는 C의 전압은 그림 8에 적히게 되는데 이는 시간은 ΔΦ/2π 만큼 차지하고 Tin의 주기를 가진다. 그리고 Ip/C1 의 전압을 가짐을 알 수 있다.
커패시터 (C1)에 흐르는 평균 전류는 아래와 같다.
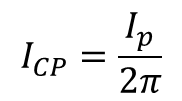
그리고 Vout은 Qa가 High 일 때 마다 증가함을 알 수 있는데 이는 Descrete time system임을 알 수 있다. 여기서 증가하는 기울기는 아래와 같다.
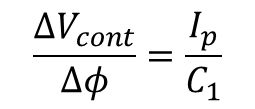
여기서 위상차가 길어지면 Turn On 되는 시간이 길어짐을 알 수 있다. 증가하는 양을 줄이고 싶으면 C를 키우면 되고, 이는 루프 대역폭을 줄이게 되는 것이다.
식 2의 평균과 라플라스 변환은 식 5와 6으로 표현할 수있다.
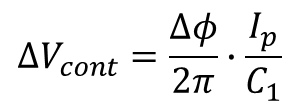
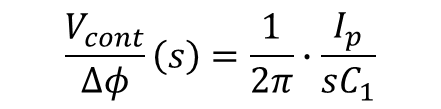
식 6이 의미하고자 한 건 무엇일까?
루프 필터는 적분기로 동작을 하게 되고 DC 주파수 일 때 무한대의 이득이 나옴을 알 수 있다. 우리가 Φin=Φout (fin=fout)일때 PLL은 Locking이 되고 두 위상의 차가 0이 됨을 알 수 있다. 따라서 ∆Φ=0 임을 알 수 있다.
루프는 입력 주파수, Kvco, Ip 상관 없이 zero static phase error를 가지며 잠긴다.
PFD/CP/C의 전달함수
위상이 변할 때 임펄스 방식의 전달함수가 되는 것이다. phase step 인풋(step function)을 구해서 실제 전달함수를 구한다음에 임펄스 함수를 구할 수 있다.
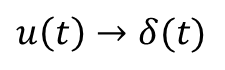
위에서 언급한 내용들을 정리해서 표현하면 아래와 같이 된다.
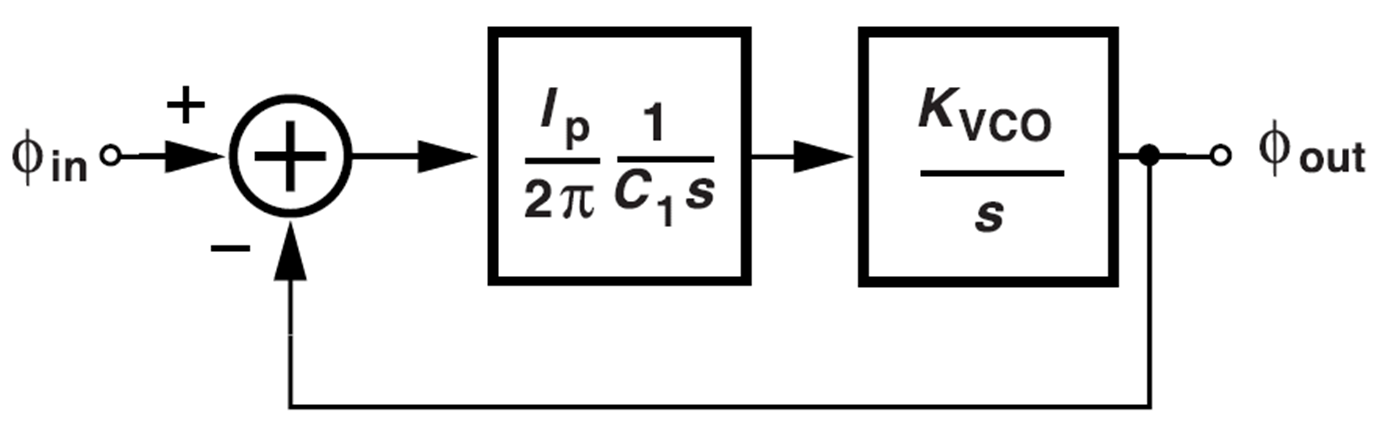
개루프 이득은 아래와 같다.
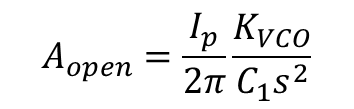
폐루프 이득은 아래와 같다.
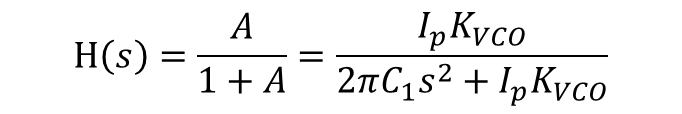
식 9를 통해 알 수 있는 점은 DC에서의 극점이 두 개가 있음을 알 수 있는데 이는 TYPE-2 PLL을 의미한다.(TYPE-1 PLL은 극점이 한개) 하지만 식 9에서는 두개의 극점이 허수축에 위치한다는 것이다. 이는 unstable 동작을 하게 된다. (ζ=0)
왜 0인지는 seconde order system 식을 보면 알 수 있는데
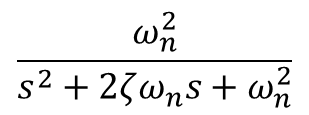
ξ : damping factor, ωn : natural freq. 이다. 따라서 식 9에서 ξ=0 임을 알 수 있다.
이에 대해 해결할 수 있는 방법은 영점을 추가해주면 해결할 수 있다. 이는 아래 그림 12와 같다.
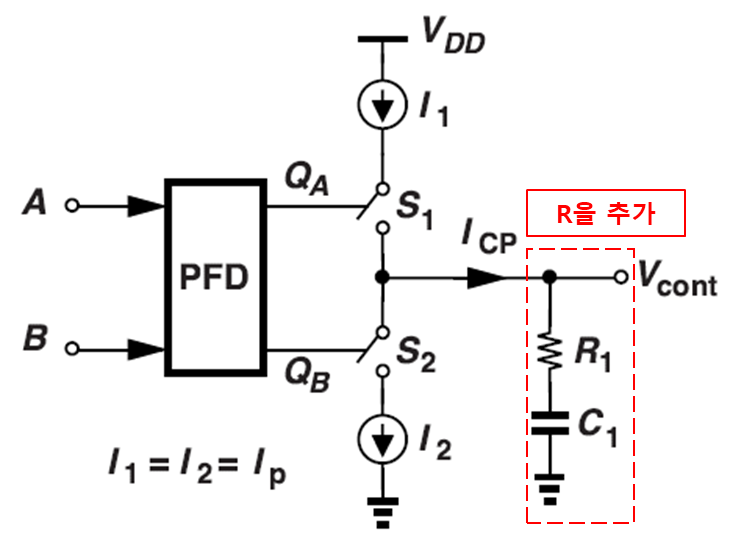
왜 직렬로 연결이 되었는지는
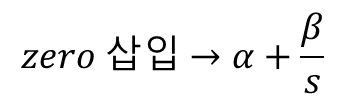
위와 같은 방법으로 하게되면 zero가 추가된다 따라서 Icp의 평균은
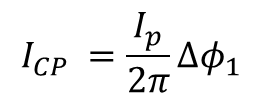
식 11임으로 Vcont는 다음과 같다.
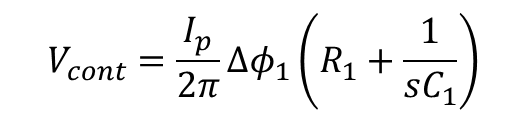
ΔΦ 만큼의 Phase 차이에 대한 Vcont의 전달함수는 아래와 같다.
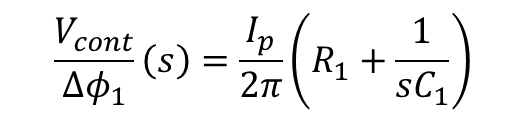
그림 11의 cp pll의 파형은 아래와 같다.

전달함수를 구하기 위해 개루프 이득을 먼저 구해보면
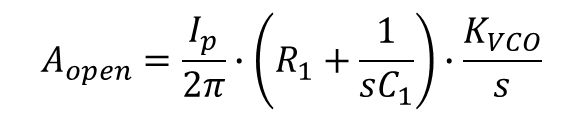
폐루프 이득은 아래와 같다.
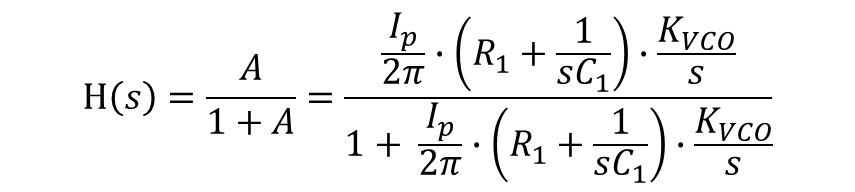
식 15를 정리하면
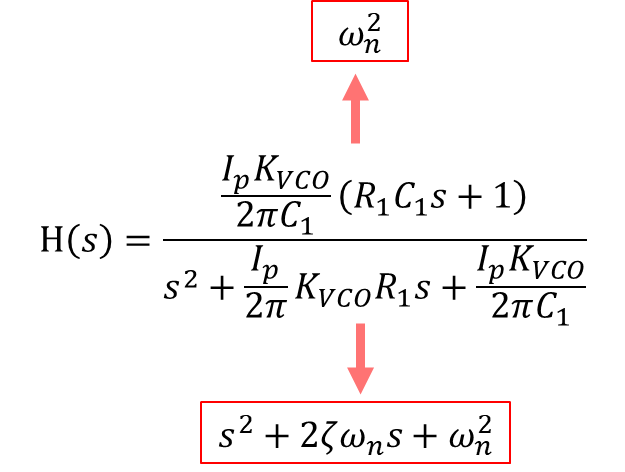
식 16을 통해 ξ (damping factor), ωn(natural freq.) 는 아래와 같이 구할 수 있다.
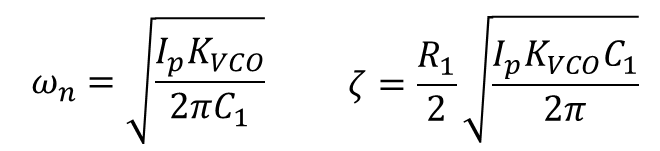
개루프와 폐루프 응답
1) Open-Loop
위상 마진(Phase Margin)에 대해서는 아래 그림 13과 같다.
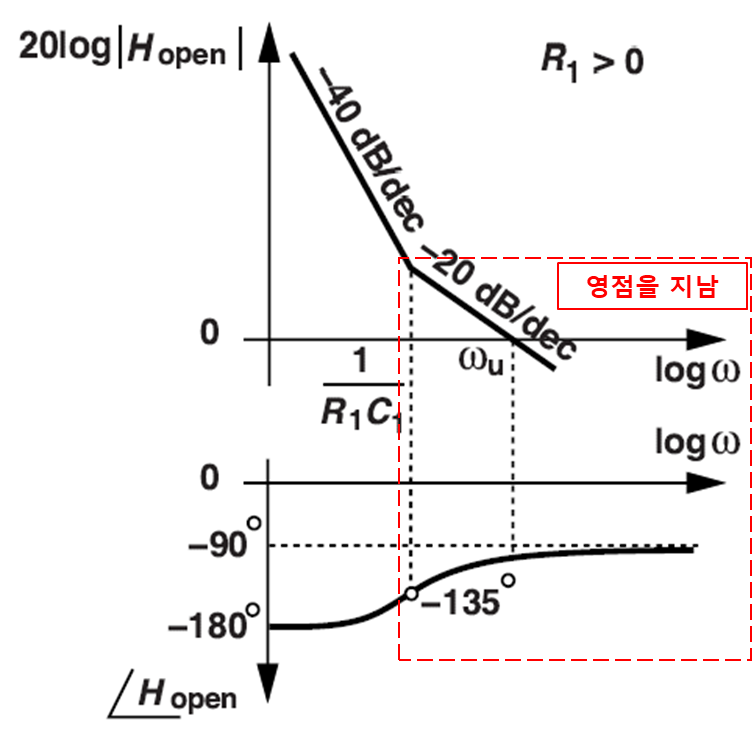
2) Closed-Loop
ξ=1 인 경우에 폐루프 응답은 아래와 같다.
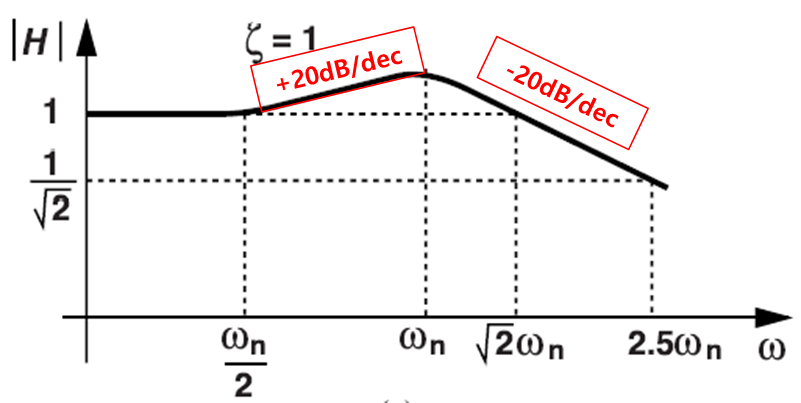
영점을 먼저 지나 +20dB/dec 의 기울기를 가지고 ωn을 지나면 -40dB/dec 를 가진다.
sampling 이론을 참조하여 최소 BW 을 위한 안정도는 fin/2 까지 만들 수 있고, 실제로는 fin/10 ~ fin/20 로 설정하는데 이는 Spur level을 줄이기 위해서이다.
CP PLL의 위상 마진 계산
시간이 모자라 추후에 내용을 채워 넣겠습니다.
PM은 아래와 같이 최종적으로 알 수 있다.
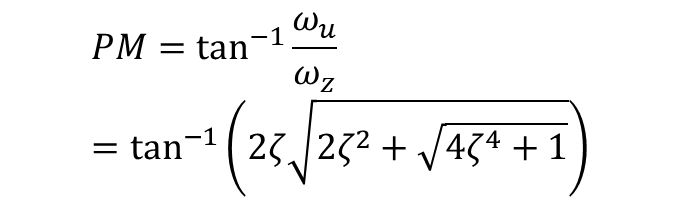
ξ에 대해서는 식 17을 따른다.
만약 M배 만큼 Divide 하는 경우 ξ는 아래와 같이 바뀐다.
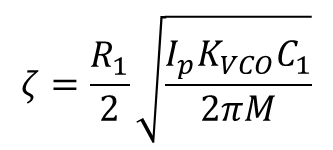
(8월 말 9월 초 추가적인 내용 작성 예정)
감사의 글
소정의 지식을 쌓는데에 도움이 되셨다면 광고 클릭을 하여 불쌍한 대학원 노예에게 10원의 기부를 부탁드립니다.
발진기, VCO와 PLL에 대한 통합 내용은
2022.03.08 - [회로 관련 전공/VCO(전압 제어 발진기)] - 전압 제어 발진기(VCO)에 대한 이론 정리
전압 제어 발진기(VCO)에 대한 이론 정리
1. 발진에 대한 개념 잡기 2022.01.19 - [회로 관련 전공/회로 과정 통합 글] - 보데의 법칙을 통해 회로의 전달함수H(s), 극점(pole), 영점(zero), 위상(Phase)을 알아보자 보데의 법칙을 통해 회로의 전달함
doctorinformationgs.tistory.com
발진기에 대한 내용은
아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.
2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼
전자회로 2 커리큘럼
전자회로 2 커리큘럼입니다. 전자회로 2에 대한 간략한 설명은 아래와 같습니다. 전자회로 1에서 배웠던 능동소자(Diode, BJT, MOSFET)에 대해 학습했으며 그에 대한 다이오드 회로 및 단일 증폭기인
doctorinformationgs.tistory.com
'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 기본 토폴로지로 구성된 1단 연산증폭기(one stage op amp) (0) | 2023.02.06 |
|---|---|
| 테브난 등가회로와 노턴 등가회로 (0) | 2023.01.27 |
| 기본 PLL(Phase-Locked Loop) 구조와 TYPE-1 PLL에 대해 (0) | 2022.07.24 |
| LC 발진기의 인덕터 모델링과 LC 발진기의 장단점 (0) | 2022.07.18 |
| LC 발진기의 주파수 튜닝과 이산 튜닝 (0) | 2022.07.18 |




댓글