출력 잡음참조 전압 예제

그림 1에서 M1에서 발생하는 잡음 전류의 구성은 아래와 같다.


출력 전체 잡음 전류는 아래와 같이 얻을 수 있다.

출력 전체 잡음 전압에 대해서는 아래와 같다.

이를 통해 알 수 있는점은 출력참조 잡음(output-reffered noise)은 직관적이지만 아래 그림 2와 같이

무잡음 증폭기가 잡음을 가지는 cs amp 뒤에 연결된 경우 무잡음 이후의 출력은 식 4에 A1 제곱이 곱해진다. 이는 이득에 영향을 받기 때문에 여러 회로의 성능을 공정하게 비교할 수 없는 문제점이 발생한다.
입력참조 잡음
(input-referred noise)
위 출력참조 잡음이 가지는 단점을 해결하기 위해 입력참조 잡음(input-referred noise)으로 회로를 해석하게 된다.
그림 1은 아래 그림 3과 같이 표현이 가능하다.

그림 3에서 표현된 모든 잡음원의 영향을 입력에서 단일 소스(source)인 잡음입력전압원으로 표현하여 아래 그림 4의 출력 잡음이 그림 3의 출력 잡음과 같게 하고, 전압이득이 존재한다면 출력 잡음 전압은 전압이득과 곱하여 표현한다.
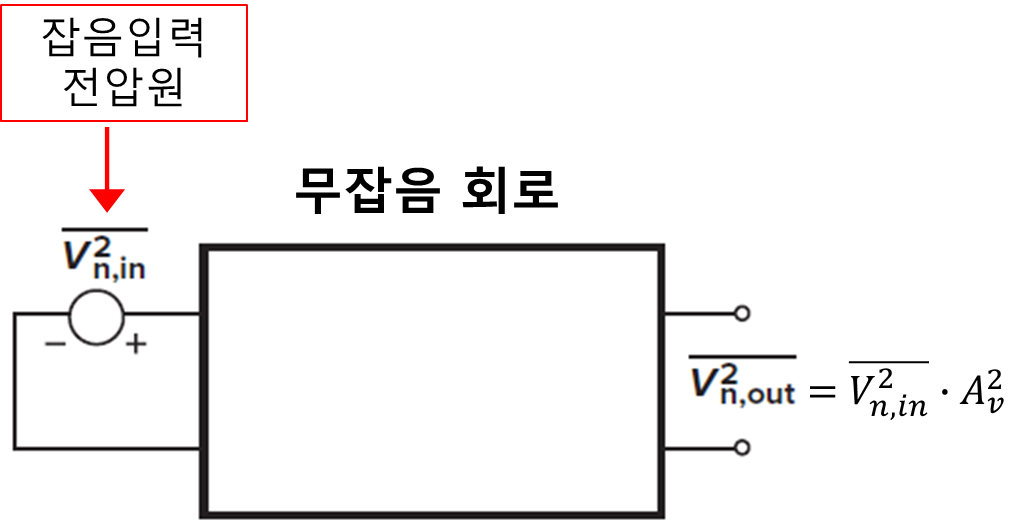
그림 1의 입력참조 잡음 전압은 아래와 같이 계산된다.
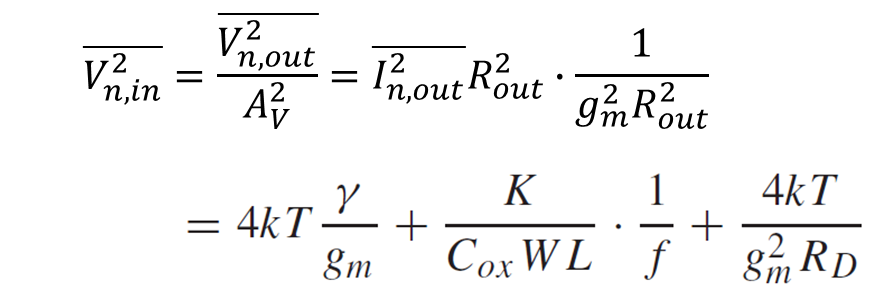
식5를 보면 알 수 있는 점은 잡음을 줄이기 위해서는 gm을 키우면 잡음을 감소시킬 수 있다.
유한한 입력 임피던스(Zin)와 유한한 전원 임피던스(Zs)를 가지고 있는 경우
아래 그림 5를 보도록 하자
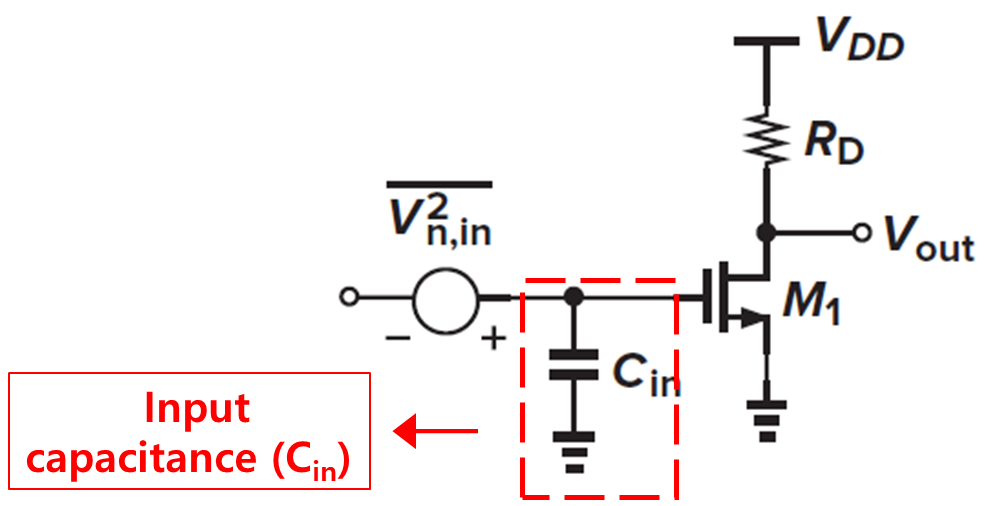
그림 5에서 Cgs, Cgd 등을 포함한 Cin이 있다고 가정하고 입력 참조 전압은 식 5로 나올 수 있지만 플리커의 잡음의 영향을 받지 않는 경우에는 아래 식 6처럼 표현이 가능하다.
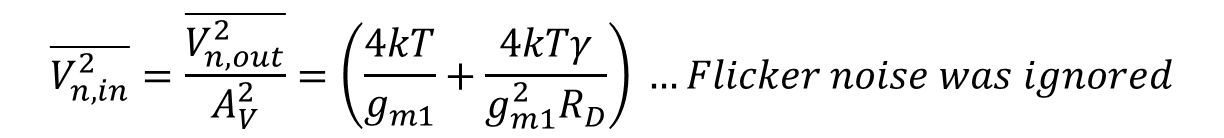
그리고 그림 5 앞에 이전 단(Preceding Stage)이 연결되어 있는경우는 아래 그림 6처럼 표현이 가능하다.
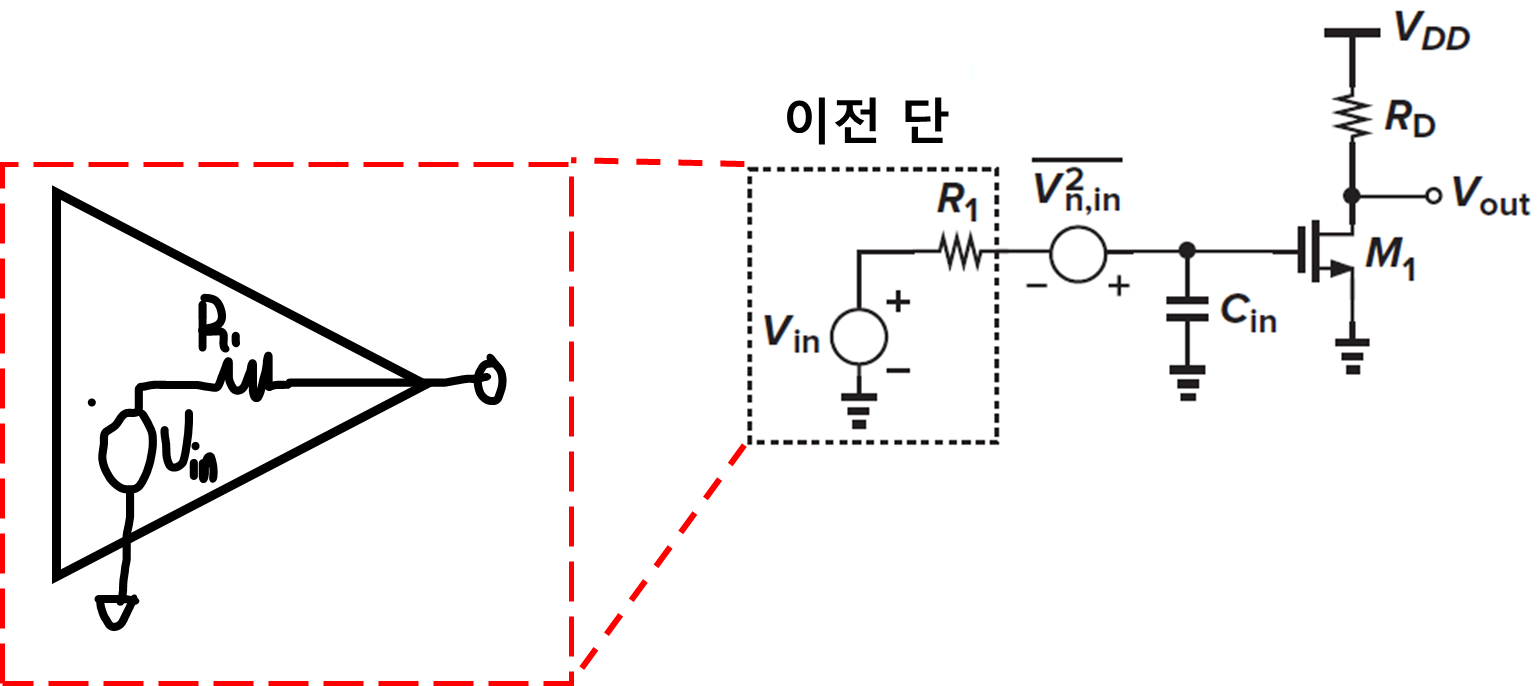
유한한 전원 임피던스(Zs=R1)의 영향으로 M1 게이트에 인가되는 전압은 R1과 Cin으로 인해 전압 분배가 걸리게 된다. 이는 식 7로 표현이 가능하다.
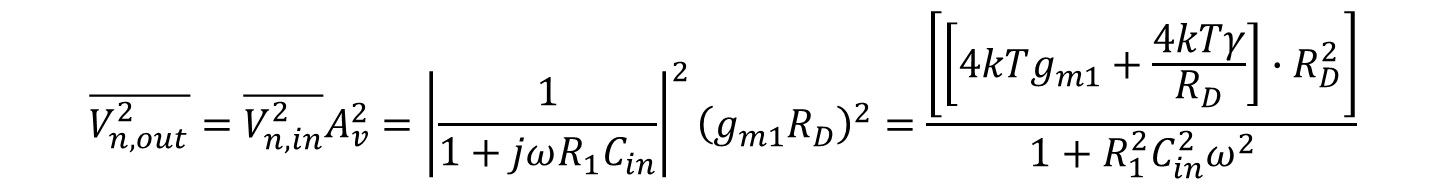
식 7의 결과를 보게되면 R1이 ∞의 값을 가지게 되면 cs stage의 출력 잡음 기여도는 0이 된다. 따라서 그림 6과 식 7의 표현은 잘못됨을 알려주고 있다. 이러한 문제점을 해결하기 위해 2단자 잡음 모델을 다루게 된다.
2단자 잡음 모델
(2-Port Noise Model)
그림 7을 보도록 하자
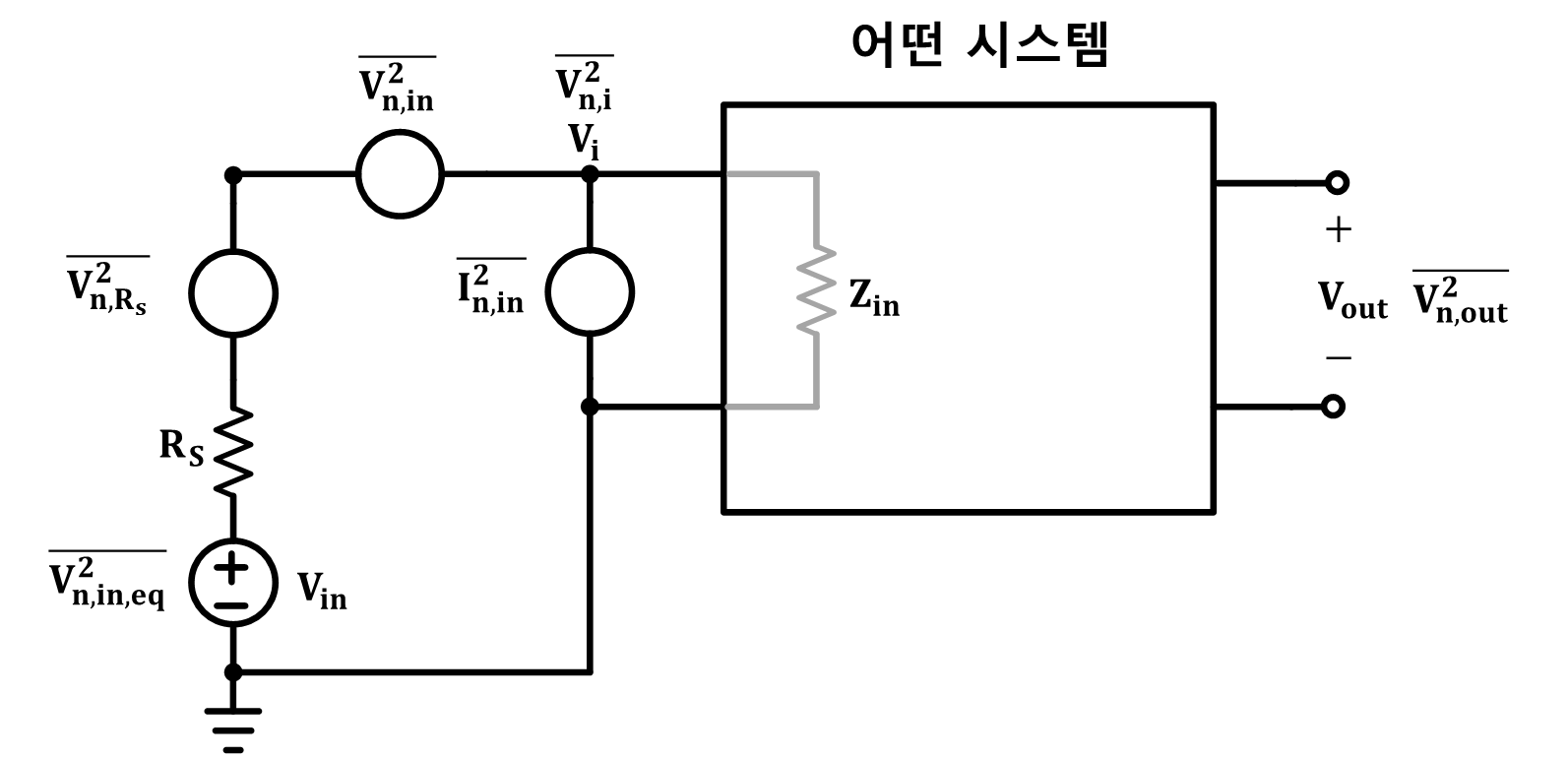
그림 7에서 시스템은 무잡음 회로와 입력 참조 잡음 전압원(Vn,in)과 병렬 잡음 전류원(In,in)으로 구성되며 같은 시스템에서 나오기 때문에 상관관계가 있지만 지금은 비상관관계라고 생각한다. Rs는 전원 내부 임피던스이고, Vin은 Signal Source 이다.
그림 7의 시스템의 이득을 (S_gain)일 때 전압 이득은 아래와 같다.
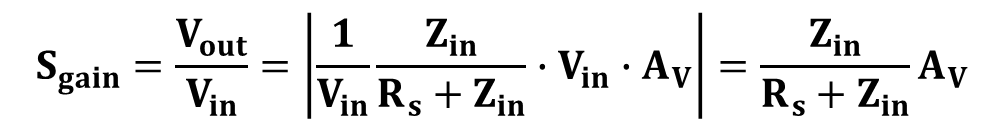
등가 입력 잡음 전압(Vn,in,eq)를 계산하기 위해 시스템쪽 입력에서의 잡음 전압은 노드 Vi에서 구할 수 있다 전압은 전압 분배식으로, 전류는 잡음 전류원과 병렬임피던스 조합으로 계산이 가능하다. 이는 아래 식 9 과 같다.
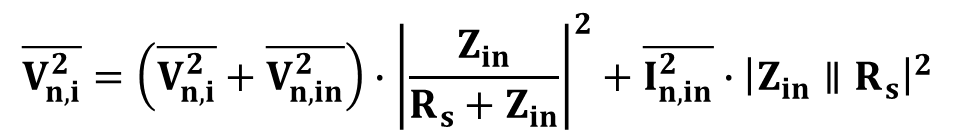
출력에서의 잡음 전압은 Vn,i (식9)와 전압이득을 곱하면 알 수 있다. 아래 식 10과 같다.
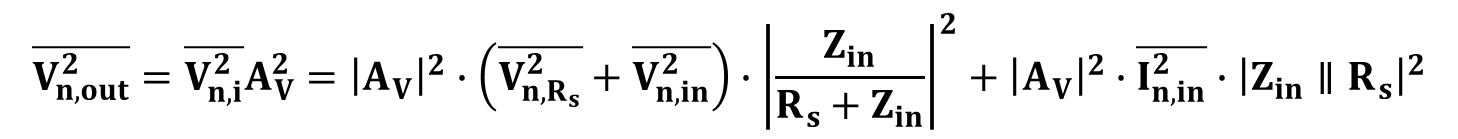
등가 입력 잡음 전압에 대해서 아래와 같이 표현이 가능하다.
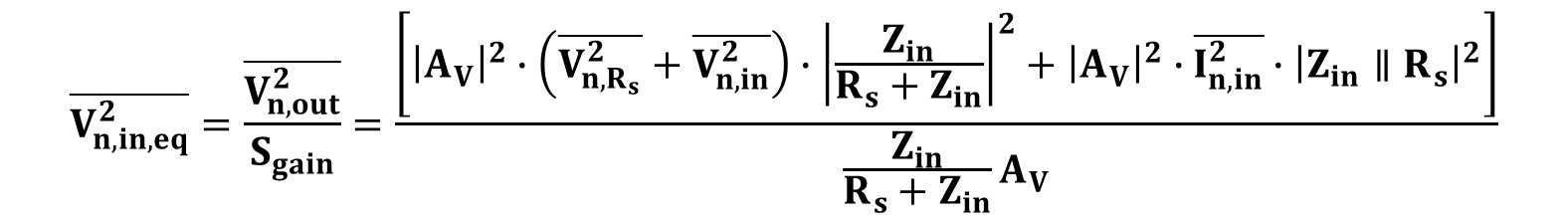
식 11을 정리한 결과는 아래와 같다.
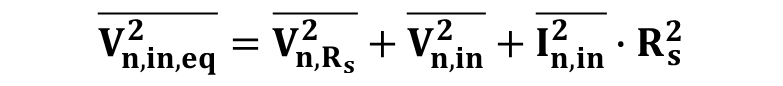
식 12를 통해 알 수 있는 점은 입력 등가 잡음 전압은 소스 저항 잡음, 시스템의 입력 잡음과 전류 잡음과 소스 저항곱의 합으로 나옴을 알 수 있다.
만약 입력 잡음 전압원과 전류 잡음 전압원이 상관 관계라면 아래와 같다.
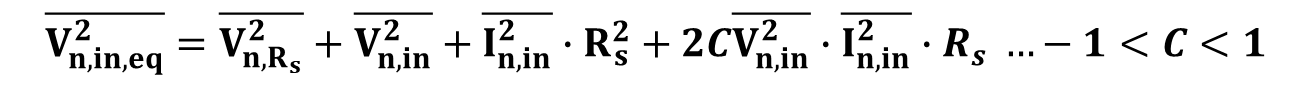
상관계수(C)는 -1 에서 1 사이의 값을 가지고 있다. -1을 가진다면 out of phase이고 1이면 in phase이다.
구해진 등가 입력 잡음 전압을 통해
1) Rs=0 인 경우
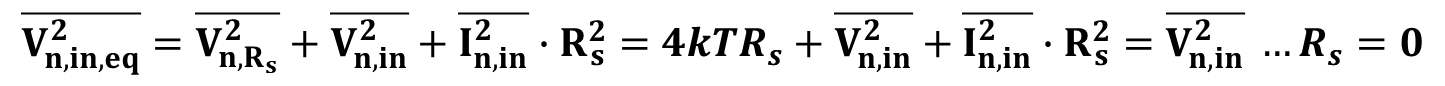
식 13은 식 5와 동일한 결과를 가짐을 알 수 있다.
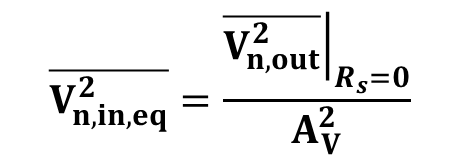
2) Rs= 무한대(∞) 인 경우
Rs가 무한대인 경우 그림 7에서의 노드 Vi에서의 전압은 Rs에 전부 걸리기 때문에 입력 잡음 전압원의 기여도는 0이 된다. 그리고 전원 내부저항과 입력 잡음 전류원 둘의 크기 차이는 입력잡음 전류원이 훨씬 크기 때문에 아래와 같은 관계를 가진다.
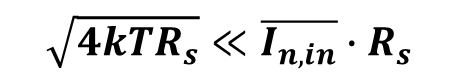
따라서 등가 입력 잡음 전압은 아래와 같다.
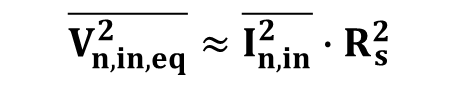
따라서 2 포트 시스템은 아래와 같이 해석 할 수 있다.
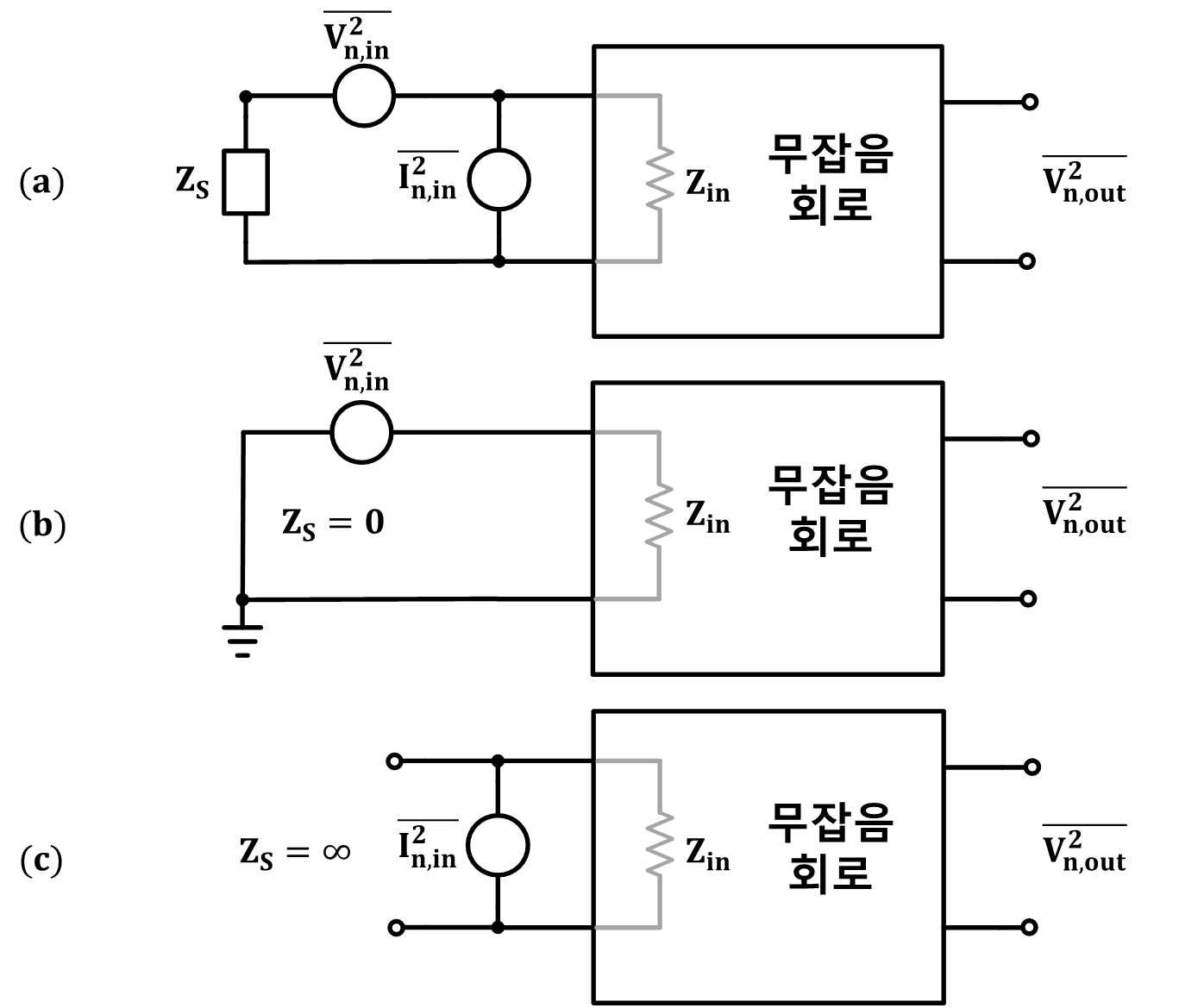
그림 6으로 다시 되돌아가 문제를 다시 해결해보도록 한다 아래 그림 9를 보도록 하자
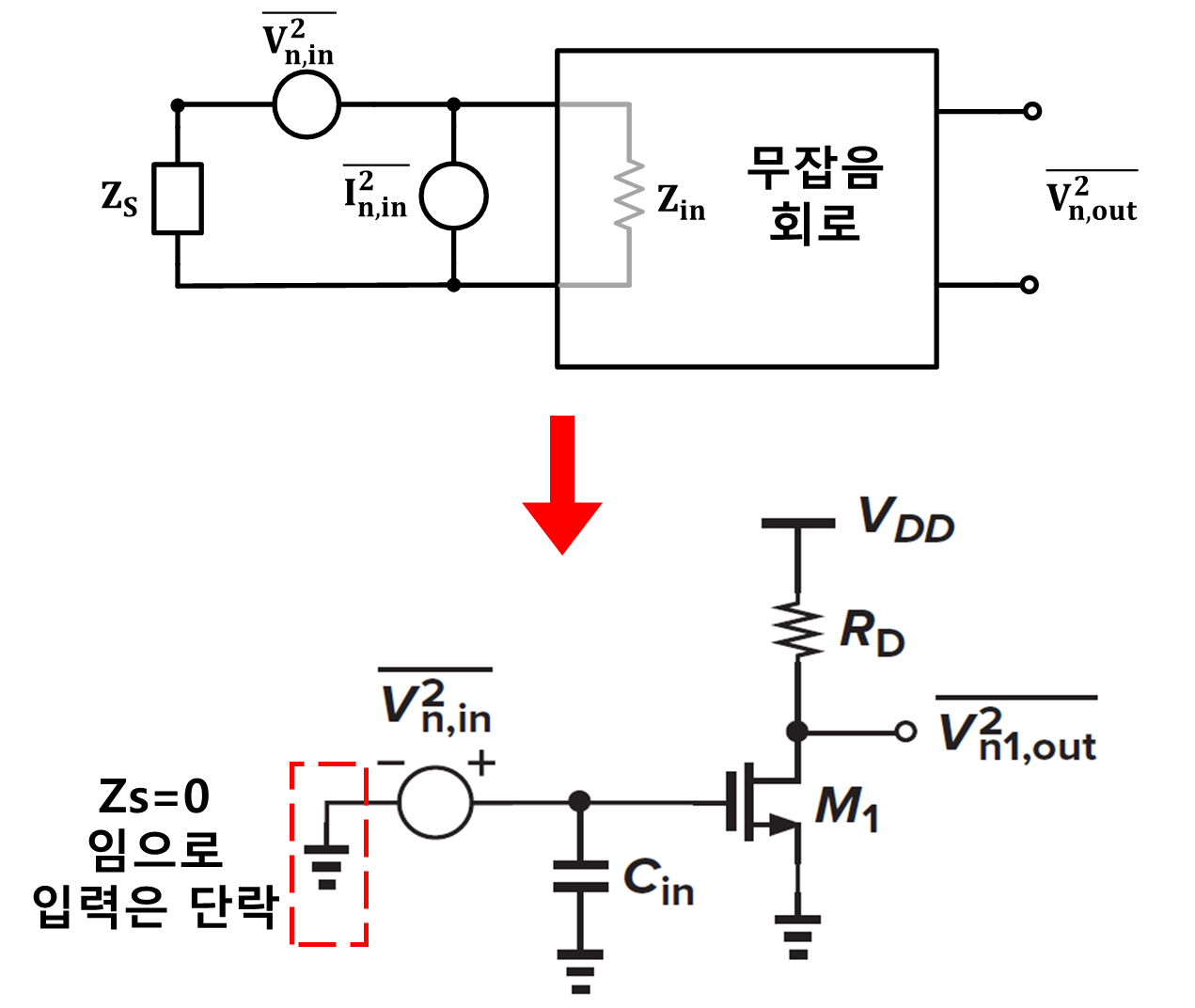
입력 참조 잡음 전압을 계산하기 위해 2단자 잡음 모델을 토대로 앞단의 소스 저항을 0으로 설정하여 계산한다 입력 참조 잡음 전압은 식 5, 6 ,14와 동일한 값으로 나오게 된다.
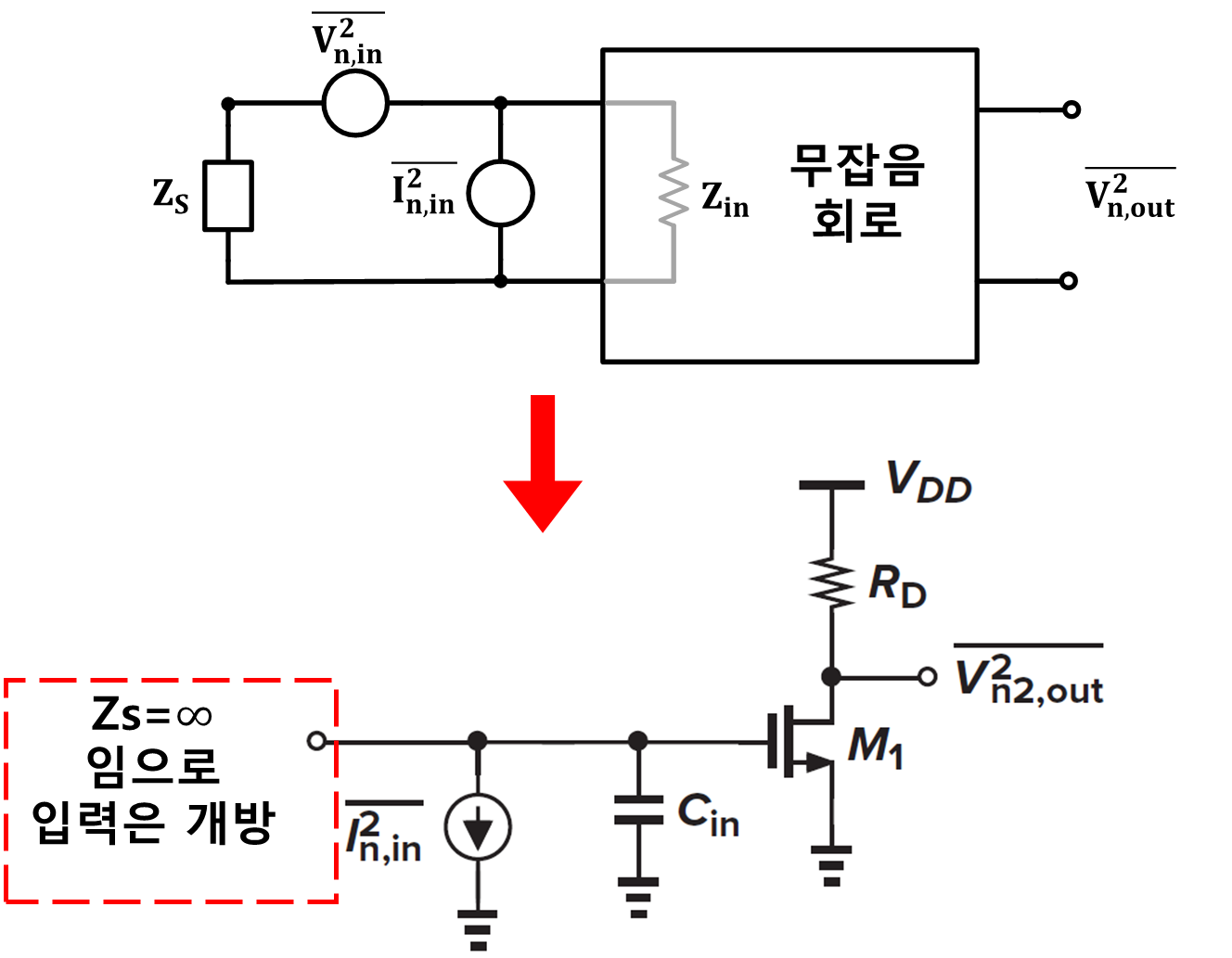
그림10 게이트에 인가된 전압을 고려한 출력 잡음 전압은 아래와 같다.
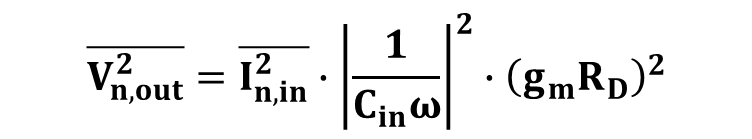
그리고 M1, RD에 의한 잡류 전류로 인한 출력 잡음 전압은 아래와 같다.

식 18은 해당 글 첫 부분에 구해졌음을 상기하자. 식 17과 18이 같고 입력 참조 잡음 전류원에 대해 계산하게 되면 아래와 같다.
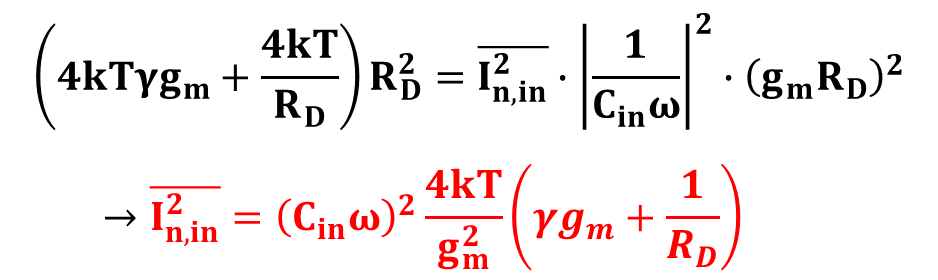
식 19와 식 6은 혼동을 가져다 준다. 이는 전류를 두번 Count해야 하는지에 대한 의문을 남기고 있다.
두 성분이 같은지 확인하기 위해 아래 증명과정을 진행해본다.
계속 작성 ~ 3월 31일까지 + 오타 수정할 것

'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| 공통 이미터 증폭기 이론(Common-Emitter Amplifier)(코어해석부터 축퇴저항까지) (0) | 2023.03.27 |
|---|---|
| BJT 바이어스 회로를 알아보자 (BJT bias circuits) (0) | 2023.03.24 |
| 슬루율(Slew Rate)과 최대 전력 대역폭(Full power bandwidth)에 대해 알아보자 (0) | 2023.03.19 |
| 대수 증폭기(Logarithmic amplifier)와 제곱근 증폭기(Square-root Amplifier)에 대해 알아보자 (0) | 2023.03.19 |
| 정밀 정류기 (Precision Rectifier)에 대해 알아보자 (2) | 2023.03.18 |




댓글