정량적인 해석에 대한 내용을 담기 위한 글이다.
전체적인 해석 플로우는 아래 링크 BJT 차동 증폭기 대신호 해석과 비슷하게 진행이 된다.
바이폴라 차동쌍의 대신호 해석(Large signal analysis of BJT differential pair)
바이폴라 차동쌍의 대신호 해석 아래 그림1 회로(바이폴라 차동쌍)을 보도록 한다. 각각의 출력 전압은 아래와 같이 볼 수 있다. 그리고 Vout에 대해서는 아래와 같이 표현이 가능하다. 그림 1에서
doctorinformationgs.tistory.com
아래 그림 1은 두 입력 차이의 원인을 가지며 그에 대한 변화(드레인 전류, 출력 전압)를 가지는데에 있어 기준이 되는 회로이다.

그림 1에서 각각의 출력 전압에 대해서는 아래와 같이 표현이 가능하다.

그리고 출력 전압(Vout)에 대해서는 아래와 같다.

그리고 Vin1-VGS1-Vp, Vin2-VGS2-Vp 루프로 KVL을 사용하게 되면 아래와 같은 결과를 얻을 수 있다.

식 3은 아래와 같이 다시 표현이 가능하다.

그리고 노드 P에 KCL을 적용하면 아래와 같은 결과를 얻는다.

식 4를 두 입력전압의 차는 각각의 VGS의 차로 표현이 가능함으로

그리고
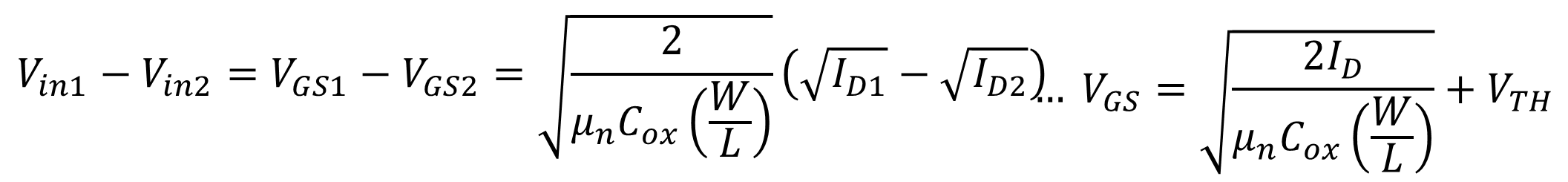
식 7을 제곱하면

그리고
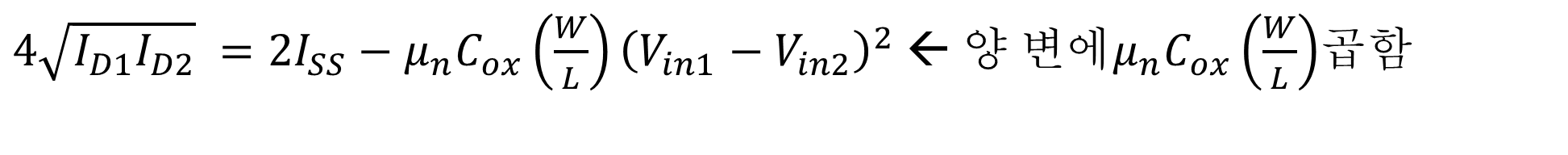
다시 제곱하게 되면
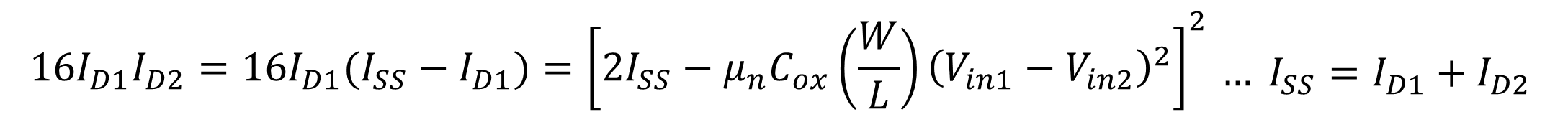
근의 공식을 사용해서 식을 전개해 다시 풀면 아래와 같이 나온다.
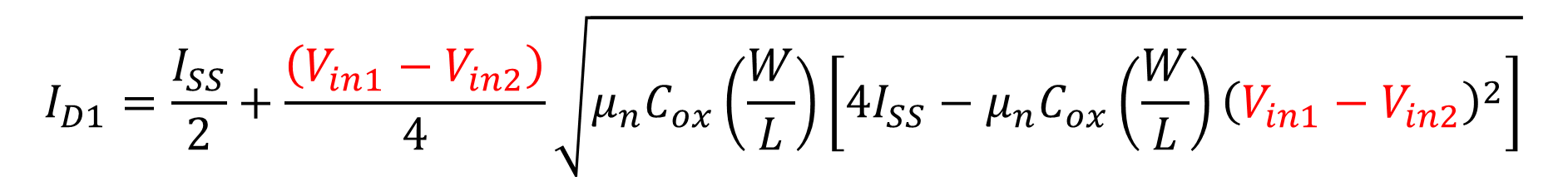
M2의 드레인 전류는 다시 식 4로부터 Vin2-Vin1 형태로 계산하게 된다면 아래와 같이 구할 수 있다.
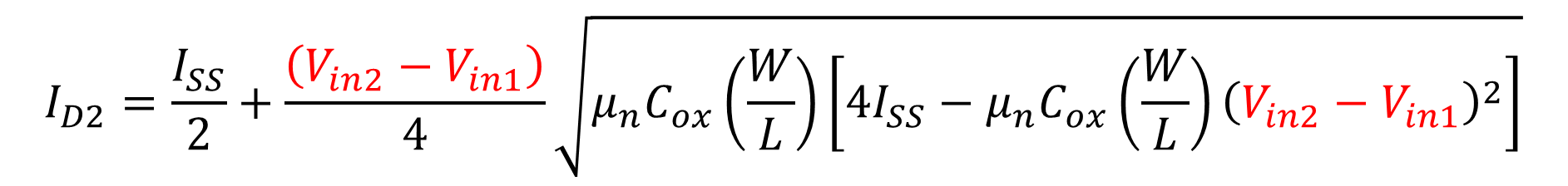
ID1-ID2의 관계로 표현하게 된다면 아래와 같다.
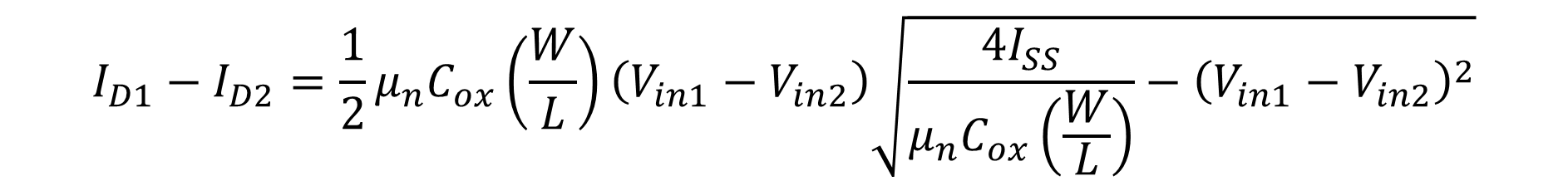
위 식 13을 통해 알 수 있는 점은 두 입력 신호 (Vin1, Vin2)의 차이가 0일 때 두 드레인 전류의 차가 0으로 떨어짐을 알 수 있다. 하지만 위 식 13은 한가지 문제점이 발생하는데 제곱근 내에 존재하는 (Vin1-Vin2)^2이 큰 값을 가지는 경우 식 13이 음의 값이 되는 것을 알 수 있다. 이는 식 13은 두 트랜지스터가 켜져 있다(Turned-on)는 가정하에 작성이 된 것이기 때문에 두 트랜지스터가 어느 지점 이상에서는 해당 식이 적용 될 수 없다.
아래 그림 1을 보도록 하자
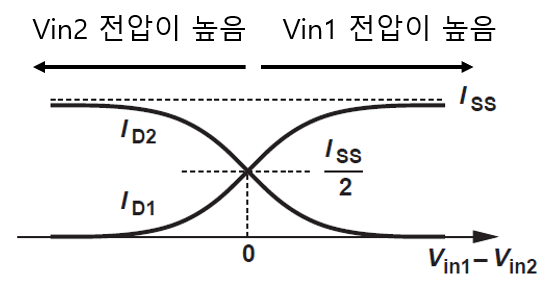
이 그림은 아래 링크에서 언급했던 내용임으로 먼저 보고 올 것을 추천한다.
2021.10.15 - [회로 관련 전공/회로 과정 통합 글] - 차동증폭기의 대신호와 소신호해석
차동증폭기의 대신호와 소신호해석
본 포스팅을 하기에 앞서 저항의 값, 트랜지스터의 사이즈(W/L)이 모두 동일하다고 가정하여 풀이를 시작합니다. 이전 진도에 대한 복습 단일 출력과 차동 출력에 대해 생기는 이점과 단점에 대
doctorinformationgs.tistory.com
한쪽이 딱 꺼지는 경우를 고려해보자 이는 차동 증폭기에서 M1 또는 M2가 꺼져있다는 것을 의미하게 되고 그림 2에서 빨간 화살표가 위치했다고 가정하게 된다면 M1이 꺼져 있음을 의미한다.
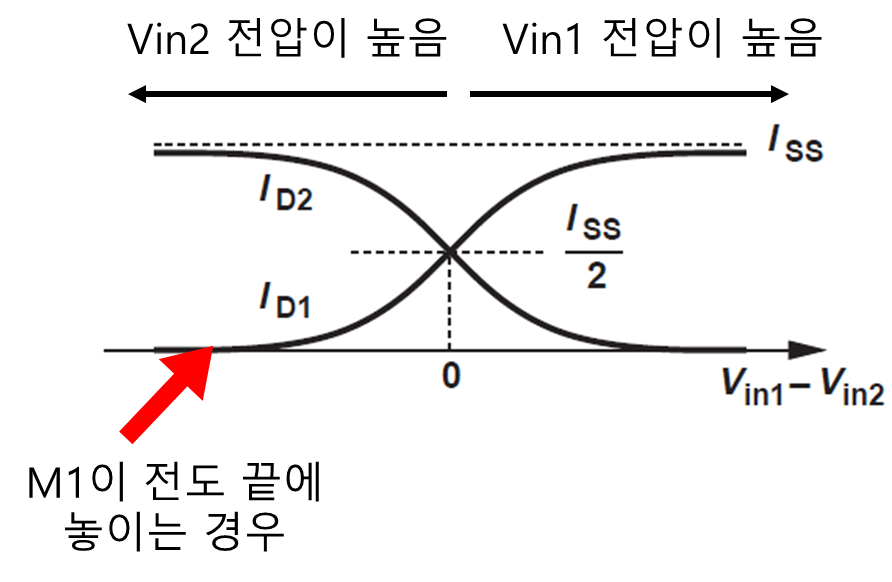
따라서 이를 수식적으로 표현하게 되면
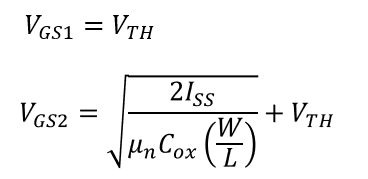
그리고 식 14를 식 4에 대입하게 되면 아래와 같은 결과를 얻게 된다.
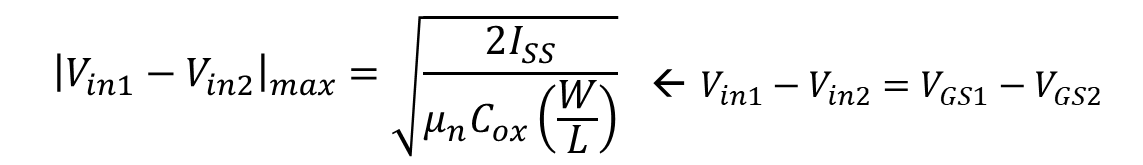
식 15에서의 max는 테일 전류원이 가지는 총 전류가 M1과 M2로 입력 전압에 따라 분배가 되었지만 두 입력 차이가 매우 양 또는 음으로 가게 된다면 한쪽이 Iss 전류를 다 가져가는 지점을 말한다.
그리고 식 15을 식 13에 대입하여 풀면 아래와 같은 결과를 가져온다.
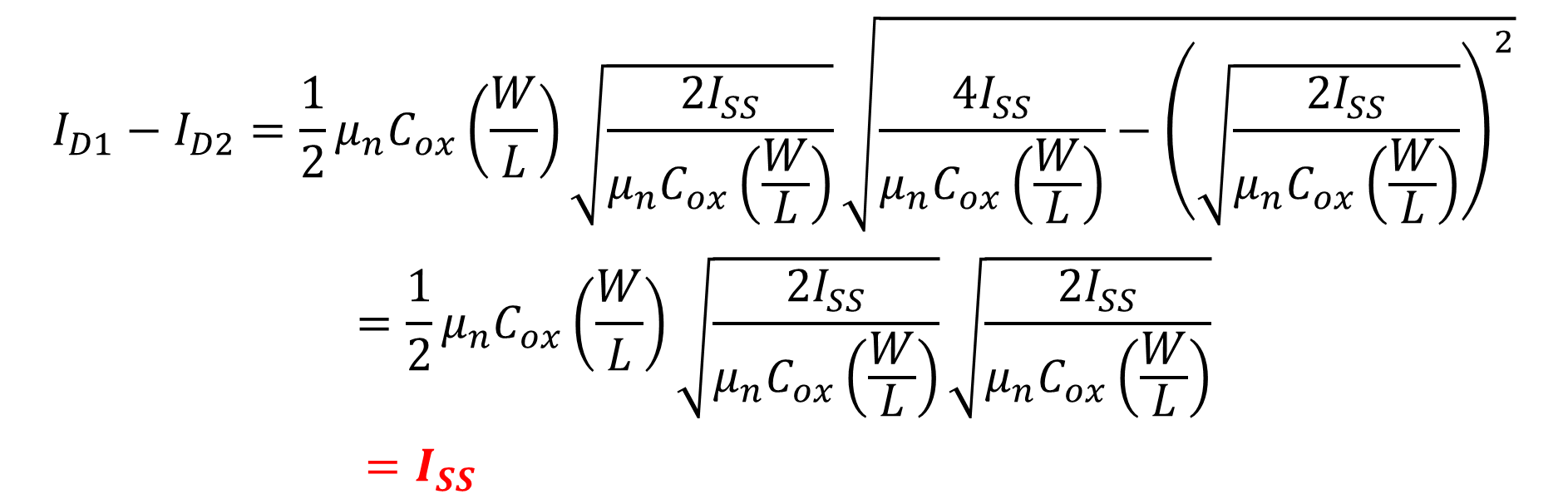
식 16을 통해 M1이 전도 끝에 도달할 때 식 16과 같이 두 전류의 차이는 Iss가 될 수 있음을 이야기한다. 반대로 M2가 전도 끝에 도달하게 된다면 식 16을 얻어지는 과정과 동일하게 Iss의 결과를 만들 수 있음을 재차 확인 하도록 한다.
그 다음으로 두 입력 전압이 같을 때의 차동 쌍은 '평형 (equilibrium)'을 가진다 입력 전압이 같을 때의 오버드라이브 전압 (Vov)는 아래와 같이 표현할 수 있다.
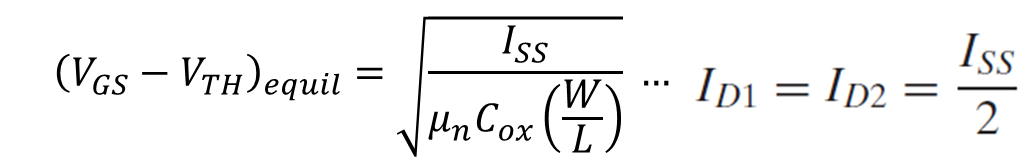
해당 식을 식 15에 대입하게 되면 아래와 같은 결과를 얻을 수 있다.
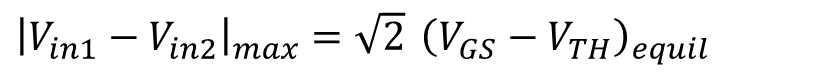
식 18은 M1 또는 M2가 모든 테일 전류를 가져오는 지점이 평형 상태(Vin1-Vin2=0)에서 루트2배 만큼 곱해진 지점임을 알 수 있다.
전자회로 2 과정을 학습하셨습니다.
아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.

2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼
전자회로 2 커리큘럼
전자회로 2 커리큘럼입니다. 전자회로 2에 대한 간략한 설명은 아래와 같습니다. 전자회로 1에서 배웠던 능동소자(Diode, BJT, MOSFET)에 대해 학습했으며 그에 대한 다이오드 회로 및 단일 증폭기인
doctorinformationgs.tistory.com
'회로 관련 전공 > 회로 과정 통합 글' 카테고리의 다른 글
| [전자회로 1] Chapter 3. 다이오드 회로와 응용 (0) | 2023.10.13 |
|---|---|
| [전자회로 1] Chapter 5. BJT 증폭기 (0) | 2023.09.15 |
| 바이폴라 차동쌍의 대신호 해석(Large signal analysis of BJT differential pair) (0) | 2023.07.11 |
| BJT 전류 거울(BJT current mirror, CM)에 대해 (0) | 2023.07.06 |
| 배전압기 또는 전압 배가기 (Voltage Doubler) 에 대해 알아보자 (0) | 2023.04.28 |




댓글