병렬 LC 탱크(Parallel LC Tank)와 손실 탱크(Lossy Tank)

해당 글은 LC 발진기를 이해하기 위한 첫 단계이다.
이전 글에서는 Q와 직렬-병렬 변환에 대해 알아보았다.

 

---

이전 진도

2022.03.26 - [회로 관련 전공/RF 설계 기초 개념] - 양호도(Q, Quality Factor)

양호도(Q, Quality Factor)

---

이번 포스팅의 목적은 병렬 LC 탱크에 대해 알아보고 LC 발진기와 연관된 1단자 관점의 발진기를 알아본다.

 

병렬 LC 탱크에서는 먼저 이상적인 LC 탱크에 대해 알아보면서 임피던스의 변화와 위상의 변화를 알아보고, 실제 LC 탱크에서는 손실 성분인 R이 있음을 알 수 있다.

 

 이상적인 LC 탱크를 만들기 위해서는 음의 임피던스(Negative Impedance) 성분이 필요함을 알고 1-단자 관점의 발진기에서 어떻게 구현해야 음의 임피던스를 만들 수 있는지 본다.

---

병렬 LC 탱크(Parallel LC Tank)

---

 

 

1) 이상적인 LC 탱크

 

아래 그림 1 회로의 입력 임피던스를 생각해 보자

 

그림 1. LC 병렬 회로

 

그림 1의 입력 임피던스는 아래의 계산 과정을 거치게 되는데

 

식 1

 

식 1을 이해하고 넘어가보자

 

그림 1의 Vin과 Iin은 어떤 정현 신호를 가진 테스트 전원으로 생각해 볼 수 있으며 L과 C로 가는 순시 전류는 0임을 생각해야 된다.

 

그림 2. 그림 1의 입력 임피던스

 

식 1에서 입력 임피던스는 ω에 대한 함수임을 알 수 있고 주파수(ω=2πf)가 DC 주파수(0 HZ)에서 증가할 수록 임피던스가 증가하다가 무한대로 올라가고, 절대값을 취한 입력 임피던스는 무한대에서 다시 떨어지게 된다.

여기서 무한대 이전에는 인덕터 성분이 지배적(dominant), 이후에는 커패시터 성분이 지배적(dominant)이다.

 

우리는 입력 임피던스가 무한대로 올라갈 때를 ω=ω1 지점을 공진 주파수라고 읽게 된다. 수식적으로는 아래와 같이 표현한다.

 

식 2

 

그림 2는 임피던스를 이야기 한 것이고 위상에 대해 도시화 하면 아래와 같이 표현이 가능하다.

 

그림 3. 그림 1의 위상 표현

 

 

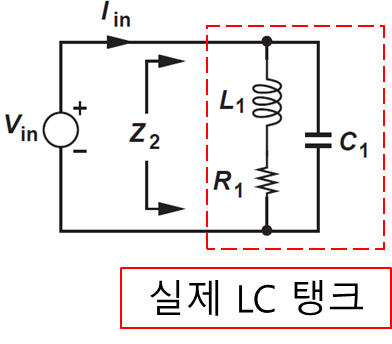
2) 실제 LC 탱크

 

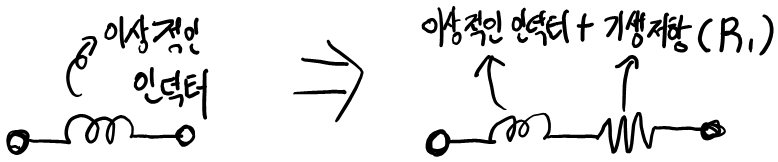
그림 1에서 표현된 이상적인 LC 탱크와 달리 실제 LC 탱크는 인덕터가 긴 도선의 형태이고 해당 도선은 저항(=기생 저항) 성분을 포함하게 된다. 이를 등가 회로로 표현한다면 인덕터와 기생 저항은 직렬 연결로 표현되고 이는 아래와 같다.

 

그림 4. 실제 인덕터의 모델링(집에서는 회로를 그리는 Visio를 못써 손으로 그림)

 

따라서 그림 4를 토대로 그림 1은 아래 그림 5와 같이 수정이 된다.

 

그림 5. 기생 저항 성분이 모델링된 실제 LC 탱크

 

기생 저항 성분으로 인해 정현 신호의 사이클마다 에너시 손실을 야기하며 손실된 에너지를 계속 보충해줘야 하며 공진 주파수 ω1에서 임피던스는 무한대보다 낮은 임피던스를 가지게 된다.

따라서 그림 5는 손실 탱크(Lossy Tank)라고 부른다.

 

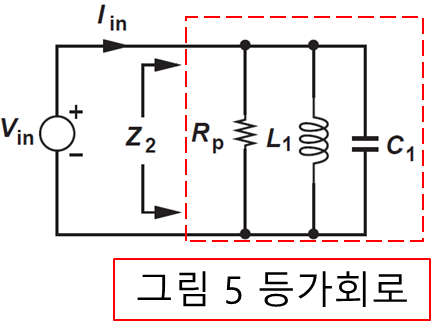
하지만 이번 포스팅의 최상단에 있는 이전 진도인 양호도에서 직-병렬 변환을 알았고 우리가 원하는 공진 주파수 (ω1) 주변의 좁은 범위에서는 아래 그림 6과 같이 변경이 가능하다

(보지 않았다면 무조건 읽을 것)

 

그림 6. 직렬 - 병렬 변환으로 얻은 그림 5의 등가 회로

 

기생 저항은 아래와 같이 표현이 가능하다.

 

식 3

 

 

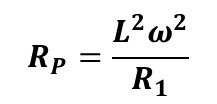
그림 6에서의 입력 임피던스 Z2(s)는 아래와 같다.

 

식 4

 

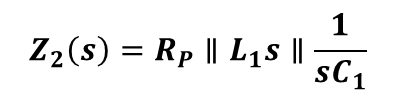
식을 풀고, s=jw로 대입하면

 

식 5

 

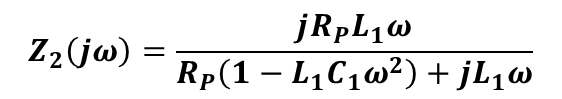
공진 주파수 (ω1)에서 (식 2참조) Z2(jw)=R_P가 되는데 이는 매우 작은 저항값이 되며 이는 그림 2와 달리 무한대의 임피던스가 아님을 알 수 있다.

 

기생 저항성분으로 인해 생기는 주파수 변화에 따른 입력 임피던스와 위상은 아래와 같이 표현 가능하다.

 

그림 7. 그림 6 회로의 임피던스 크기와 위상

 

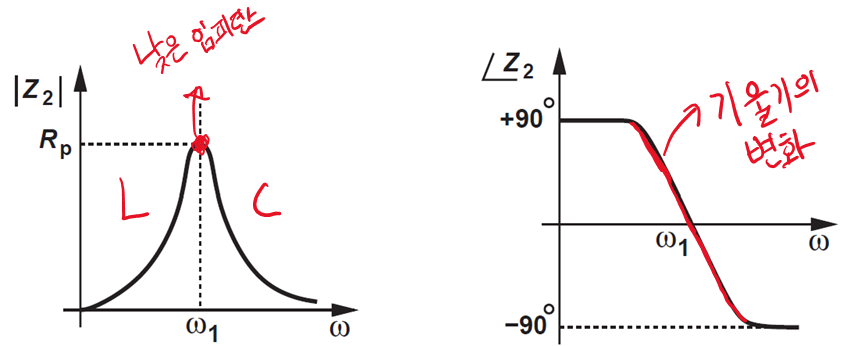
따라서 실제 LC 탱크 회로는 Rp 성분을 없애기 위해 다음 진도인 1-단자 관점에서의 발진기를 알아보도록 한다.

 

---

감사의 글

 
소정의 지식을 쌓는데에 도움이 되셨다면 광고 클릭을 하여 불쌍한 대학원 노예에게 10원의 기부를 부탁드립니다.

 

발진기, VCO와 PLL에 대한 통합 내용은

2022.03.08 - [회로 관련 전공/VCO(전압 제어 발진기)] - 전압 제어 발진기(VCO)에 대한 이론 정리

전압 제어 발진기(VCO)에 대한 이론 정리

발진기에 대한 내용은

아래 링크를 통해 다음 진도와 전자회로 2의 모든 내용을 확인하실 수 있습니다.

2022.01.12 - [전공(Major)/전자회로 2 과정] - 전자회로 2 커리큘럼

전자회로 2 커리큘럼

---