용어 이해

| 표 1. 회로를 이해하는데에 도움을 주는 용어 설명 | ||
| 명칭 | 정의 | |
| 가지(Branch) | 두 마디(Node)를 연결하는 경로(Path) | |
| 필수 가지 (Essential Branch) |
1개의 필수 마디(Essential Node)도 통과하지 않고 2개의 필수 마디를 연결하는 경로 | |
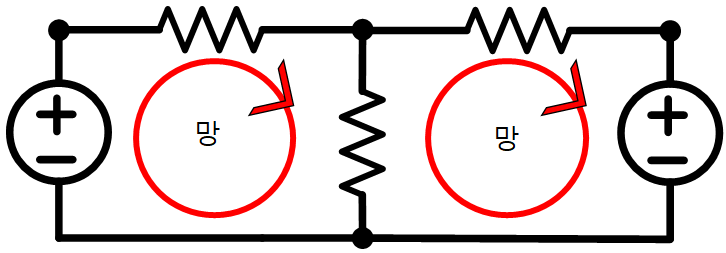
| 망(Mesh) | 다른 폐회로와 겹치지 않는 폐회로 | |
마디와 필수 마디에 대해 잘 이해가 가지 않으신 분들은 아래 링크에서 마디와 필수 마디에 대한 표현 부분만 읽고 돌아오시면 됩니다.
2021.07.30 - [전자회로의 이해/Basic] - 마디 전압법과 초 마디(Super Node)
마디 전압법과 초 마디(Super Node)
머 릿 말 KCL, KVL을 지난시간에 배움으로써 회로를 해석하는데에 있어 필요한 도구 중 하나를 배웠고 이번에는 마디 전압법과 초 마디(Super Node)를 알아보도록 하겠습니다. 회로를 해석하는데 있
doctorinformationgs.tistory.com
망 전류법
기초적인 설명은 헤이트 교재

망 전류법은 필수가지-(필수 노드 -1)개의 방정식으로 회로를 해석하도록 합니다. 위에 용어정리에서 필수가지, 가지, 망에 대해 이미 알고 있음으로 필수 노드를 표기하면 2개가 나옵니다.
즉 3개의 필수 가지와 2개의 필수 노드로 방정식의 개수는 아래와 같습니다.

필수 노드 - 1 이므로 1 개의 독립 전류 방정식을 사용할 수 있다. 윗 부분에 필수 노드에 KCL을 적용하면 아래와 같습니다.

여기서 위 회로를 자세히보면 두 폐회로에 KVL을 적용하게 되면 시계 방향(또는 반시계)로 회전할 때 겹치는 가지(Branch)가 있음을 확인할 수 있습니다.
바로 I3임을 확인 할 수 있는데 I3에 대해 식 (2)를 살짝 바꿔주면 아래와 같습니다.

위 회로에서 두 폐회로에 KVL을 적용하면 아래와 같습니다.



식 5에서 음의 기호가 붙은건 폐회로를 회전하는 방향이 R3를 지날 때 전압 상승을 겪기 때문에 음의 부호로 표기가 됩니다.
(Chapter 1 에서 전류의 값이 양인 경우는 전압 강하를 하고 있다는 의미로 볼 수 있음으로 위 회로를 아래와 같이 표기 할 수 있습니다.)
2021.07.13 - [전자회로의 이해/Basic] - 전압과 전류, 전력과 에너지 / 회로이론 기초
전압과 전류, 전력과 에너지 / 회로이론 기초
오늘은 전압, 전류의 개념들은 공학적인 관점에서 유용한데, 전압과 전류를 정량적으로 표현 가능하기 때문이죠 그리고 전력, 에너지에는 전압 및 전류가 회로를 해석과 설계에 대해 유용하지
doctorinformationgs.tistory.com
식 4와 5에 식 3을 대입하여 계산하면 아래와 같습니다.


마지막 계산결과도 중요하지만 중간에 전류의 차 부분이 망 전류법에 중요하니 꼼꼼히 확인 하시기 바랍니다.
식 2번부터 식 7번까지 우리는 3개의 연립 방정식의 해를 2개의 연립 방정식으로 바꾸어 놓기 위해서 위의 과정을 거쳤는데 망 전류법을 사용하면 간단하게 식 1과 같이 2개로 바로 표현하여 앞선 계산 과정에 비해 빠르고 편리하게 사용할 수 있습니다. 즉 망 전류법에서는 필수 노드-1 의 전류 방정식을 제거 할 수 있습니다.
위 회로에서 설명된 것과 다르게 폐회로에 I_A 와 I_B의 전류가 흐른다고 생각하고 KVL을 적용합니다.
그런데 R3에 흐르는 전류는 A, B 전류가 겹치는 것을 알 수 있죠
이럴 때는 KVL을 적용했을 때의 기준이 되는 전류가 양의 기호를 가지게 됩니다 식 (8) (9)의 빨간 표시를 보게 되면 식 8은 왼쪽에 있는 폐회로에 KVL을 적용했기 때문에 I_A가 양의 값을 가지고 I_B만큼을 빼주게 됩니다.
식 9는 오른쪽 폐회로에 KVL을 적용했기 때문에 I_B가 양의 값을 가지고 I_A만큼 빼주게 되는 것이죠
따라서 KVL을 어디에 적용이 되고 어떤 전류가 기준점이 되냐는 것입니다.

망 전류법은 폐회로에 KVL을 적용을 시키는 것인데 폐회로에서 망(MESH)의 표현은 마치 폐회로 내에 흐르는 전류가 전압 강하 또는 상승을 겪으면서 KVL의 식을 만들어 주는 것처럼 생각할 수 있어요


식 (6, 7)과 식 (8, 9)는 동일한 형태임을 알 수 있고 전류를 다시 정리해 보면 아래와 같습니다.

슈퍼 메시
슈퍼 메시(Super mesh)의 개념을 사용함으로써 미지 전압 v를 도입하지 않을 채 회로 해석을 할 수 있습니다.
슈퍼 노드(초 마디, Super Node) 전압원을 제거하지만 슈퍼 메시 같은 경우에는 전류원을 제거하여 해석을 하게 됩니다.
이제 아래의 전류원과 전압원이 값이 있는 회로를 통해 해석을 해보도록 할게요.

자 여기서 필수 가지에 대해서 6개인데 왜 5개 인지 의문을 가지실 수 있을텐데 노드 b에서 KCL을 적용해 볼게요.


이 전류원의 존재로 인해서 Ia와 Ib의 차이가 6A로 제한되기 때문입니다. 따라서 필수가지는 5개를 가지며 2개의 망 전류 방정식을 가지게 되는 것입니다.
위 회로에 대해 모든 값을 넣고, 전류원을 없애는 슈퍼 메시를 적용하게 되면 아래와 같습니다.

슈퍼 메시를 적용하여 KVL을 하게 되면 아래와 같은 식이 나옵니다.

식 13을 전개해서 풀면 아래와 같습니다.

Ic로 KVL을 적용하고, 식을 정리하면 식 15와 16이 나오게 됩니다.


슈퍼 메시와 KVL을 통해 식 13과 15를 얻게 되는데 이 두식으로 풀 수 없으니 KCL을 적용해서 6 A로 제한했었던 식 12를 통해 계산을 하게 되면 최종적으로 아래의 값을 얻습니다.

만약에 슈퍼 메시를 적용하지 않고 계산을 하게 되었다면 얼마나 더 번거로운 과정이 있는지 간략하게나마 적어보겠습니다.
망 Ia, Ib, Ic에 대해 KVL을 적용하면 식 3개가 나오게 되고, 노드 b에 KCL을 하여 식 한개가 더 나와식을 정리하기까지 4개의 식으로 회로를 해석해야 됩니다.
하지만 슈퍼메시를 적용함으로써 식 12, 13, 15로 세개의 식이 나와 식이 하나 더 없는 식으로 회로를 해석할 수 있는 장점이 있는 것이지요
이 글의 하단에 있는 공감버튼(❤️)을 눌러주시면 포스팅을 쓰는데 더 좋은 원동력이 되고
블로그의 구독은 최신 정보를 실시간으로 받을수 있습니다.

감사합니다.
'회로 관련 전공 > Basic' 카테고리의 다른 글
| 중첩(Super Position)의 원리 (0) | 2021.08.18 |
|---|---|
| 전원 변환에 대해 알아보자 (0) | 2021.08.18 |
| PDF리더로 논문 제일 효율성 높게 읽는법 (2) | 2021.08.06 |
| 마디 전압법과 초 마디(Super Node) (3) | 2021.07.30 |
| 저항회로와 전압분배 전류 분배에 대해서 알아보자 (0) | 2021.07.24 |




댓글