중첩, 간략한 서론
회로이론이라는 과목을 하면서 중첩을 도대체 "왜? 어디서? 써먹는거지?" 라는 의문이 들 수 있습니다.
하지만 우리는 두 개이상의 전원을 사용한 회로(브레드 보드 or 빵판)를 실험했을 때 어떤 가지(branch)에 전류 또는 전압을 측정했을 때 중첩이 된 값을 측정했었던 것을 알 수 있었죠.
(전류를 올바르게 측정한거 같은데... 전류의 방향이 반대의 값을 가진 것을 확인한다던가, 전압의 값이 다르다는 것도)
우리는 여러가지 실험을 통해서 중첩이 된 값을 중첩의 원리를 통해 회로 해석으로 각 전원이 얼마만큼의 전압, 전류가 인가되는지 알 수 있기 때문에 중첩을 통한 회로 해석을 하는 겁니다.
전압원-전류원 예시 회로를 이해하면 다른 전원인 전압원-전압원, 전류원-전류원 회로도 충분히 이해 할 수 있어 전압원-전류원 회로를 선택했습니다. 중첩에 대해서 완벽히 알아보도록 하죠
중첩의 원리
선형 시스템은 중첩의 원리를 따르게 됩니다. 여기서 회로에서의 선형이라함은 흔히 우리가 다루는 수동 소자(Passive element)인 저항, 인덕터, 커패시터를 이야기합니다.
예를 들어서 저항을 생각해보면 저항에 걸리는 전압은 전류와 저항에 비례(V=IR), 전류는 전압에 비례하고 저항값엔 반비례 하는 것을 알 수 있습니다.
결국 이 비례함을 선형이라고 생각할 수 있죠.
결국 중첩의 원리는 선형 시스템이 하나 이상의 독립 전원에 의해 여기(Excitation)되거나 구동이 될 때 회로망에 있는 전체 응답은 개별(또는 각각의) 응답의 합으로 표현할 수 있습니다.
이해를 돕기 위해 개별 응답은 하나로만 동작하는 독립 전원의 응답입니다.
여러개의 독립 전원이 있는 회로를 한번에 해석하기 어려움으로 하나씩 하나씩 회로의 응답을 합성하여 결과를 알아내게 됩니다.
독립 전원이 전압-전류로 구성된 예시 회로를 알아보도록 할게요.
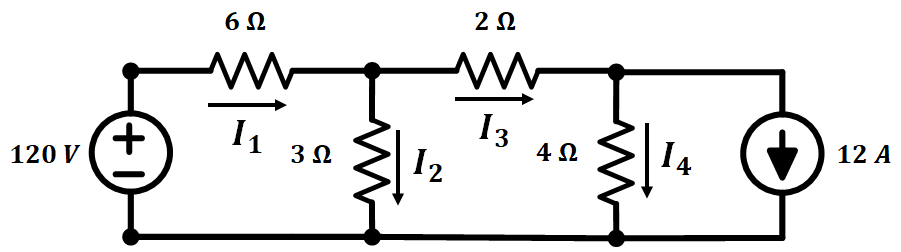
예시 1 회로에서는 4개 가지에 흐르는 전류를 알기 위한 것인데요. 현재 전원 2개인 전압원, 전류원으로 구성이 되어있습니다.
전원 변환포스팅에서 배웟듯이 전압원은 전압 강하가 이루어 지지 않게 단락(쇼트, Short)시켜야 전류원 입장에선 하나의 전원으로 볼 수 있고, 전류원은 전류가 흐르지 않게 개방(오픈, open)이 되야 전압원 입장에서 하나의 전원으로 해석이 가능하게 됩니다. 즉 각각 전원을 개방과 단락 시켜 2번의 회로 해석이 필요하게 되는 것이죠.
2021.08.18 - [전자회로의 이해/Basic] - 전원 변환에 대해 알아보자
전원 변환에 대해 알아보자
회로를 해석하는 방법중에서 여러가지 방법이 있습니다. 맨 처음 KVL과 KCL에 대해 기초를 닦고 그 다음 노드 전압법과 망 전류법을 통해서 조금 더 해석하는 방법을 찾았었죠 이것들 외에도 여러
doctorinformationgs.tistory.com
먼저 전류원을 개방시켜 전압원을 통해 흐르는 전류를 해석해보겠습니다.
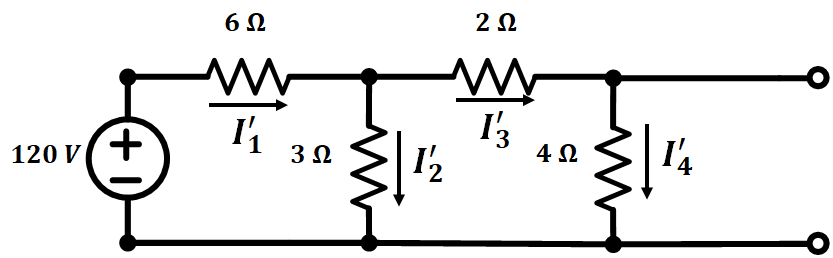

위 회로를 보게 되면 I의 전류 표기에서 (')이 붙은 것을 알 수 있는데 이는 중첩 과정에서 계산 할 때 몇번째 순서의 값을 표기한 것을 의미하게 되는데요 현재 위 회로에는 2개의 전원이 있고 두 전원에서 각각 계산을 하니 2번의 계산이 필요하게 됩니다.
따라서 첫번째 해석으로 전류원을 개방하여 계산할 때는 I' 이 붙게되고 두번째 해석으로 전압원을 단락 시킬 때 I''이 되게 됩니다.
만약에 3개의 전원이 있고 세번째 중첩에 대해 해석을 할 때 I''' 이 붙게 되는겁니다.
각각의 (')과 ('')을 계산하고 각각 브랜치에 흐르는 전류를 합하면 중첩 계산이 끝나게 됩니다.
위 사진 (좌) 회로는 (우)와 등가로 표현이 가능하고, 따라서 2옴과 4옴은 직렬 저항으로 표현이 가능합니다. 노드 a에서 KCL을 적용함으로써 아래와 같이 표현이 가능합니다.

V에 대해 식을 풀게 되면 V는 30 볼트의 전압을 가지게 되어 노드 a의 전압 강하는 30 V를 가진다는 것을 알게 되죠

노드 a에 걸리는 전압 강하가 얼마나 나왔는지 알기 때문에 식 (1)에 V를 대입하여 각각 브랜치에 흐르는 전류를 알 수 있습니다.

식 3에서 전압의 표기가 식(1)의 좌측 (I1)' 의 전압의 값의 순서가 바뀐 이유는 전류의 방향이 120V -> 30V로 가기 때문에 (120-30)/6 으로 계산이 됩니다.
식 (1)은 노드 a를 기준점을 삼아 KCL을 계산을 한 것이니 혼동하지 마시길 바랍니다.
이 부분이 어렵다면 아래의 링크를 읽고 돌아오시길 바랍니다.
2021.07.22 - [전자회로의 이해/Basic] - 키르히호프 전압, 전류 법칙 완벽히 알아보자
키르히호프 전압, 전류 법칙 완벽히 알아보자
머 릿 말 안녕하세요 배고픈 노예입니다. 회로이론 또는 전자회로 외 논문이나 여러가지 전자공학과 관련 서적을 보게되면 키르히호프 전류, 전압 법칙은 회로해석을 하는데에 있어서 항상 필
doctorinformationgs.tistory.com
2021.07.30 - [전자회로의 이해/Basic] - 마디 전압법과 초 마디(Super Node)
마디 전압법과 초 마디(Super Node)
머 릿 말 KCL, KVL을 지난시간에 배움으로써 회로를 해석하는데에 있어 필요한 도구 중 하나를 배웠고 이번에는 마디 전압법과 초 마디(Super Node)를 알아보도록 하겠습니다. 회로를 해석하는데 있
doctorinformationgs.tistory.com
나머지 전류는 아래와 같습니다.
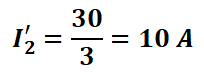

여기까지가 전류원을 개방한 상태에서 KCL을 통해 미지의 전압을 계산했고 해당 전압을 통해 전류를 구했습니다.
이제 두번째 해석인 전압원을 단락시켜 ('')의 전류를 구해보겠습니다.

위 전압원을 단락시킨 회로는 필수 노드가 2개임으로 마디 전압법을 통해 해석할 수 있습니다. 하단의 빨간 화살표는 기준 마디를 의미하는 것입니다.
따라서 기준마디로 부터 2개의 미지 전압 (V1, V2)가 나오게 되고 마디 전압법을 통해 계산을 하게되면 아래와 같습니다.
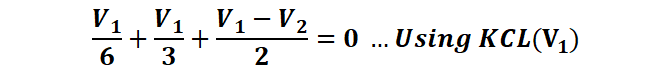

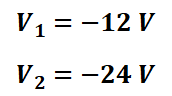
기재된 전류의 방향을 참고하여 I''에 대해 계산하면 아래와 같습니다.

식 (9)의 경우는 (I1)'' 이 좌측은 단락된 전압원이므로 0V를 가지고 있습니다. 따라서 좌에서 우로 향하는 전압은 0-V1이게 된 것이죠.
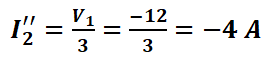

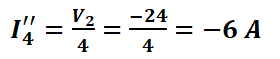
개별 전원의 합은 전체 응답이므로 계산했던 전류는 아래와 같습니다.

식 (13)을 토대로 예시 회로에 값을 넣고 적용하면 회로는 다음과 같이 표현이 가능합니다.

I4는 음의 값을 가졌으므로 반대의 방향을 가지게 됩니다.
이 글의 하단에 있는 공감버튼(❤️)을 눌러주시면 포스팅을 쓰는데 더 좋은 원동력이 되고
블로그의 구독은 최신 정보를 실시간으로 받을수 있습니다.

감사합니다.
'회로 관련 전공 > Basic' 카테고리의 다른 글
| 트랜스컨덕턴스(gm)의 의미 (0) | 2021.10.09 |
|---|---|
| 입출력 임피던스는 왜 필요할까? (0) | 2021.10.07 |
| 전원 변환에 대해 알아보자 (0) | 2021.08.18 |
| 망 전류법과 슈퍼 메쉬 (0) | 2021.08.06 |
| PDF리더로 논문 제일 효율성 높게 읽는법 (2) | 2021.08.06 |




댓글